MHB Find a formula for the Riemann sum and take the limit of the sum as n->infinite

[tornado711]

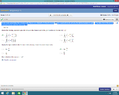
For the function given below find a formula for the Riemann sum obtained by dividing the interval [1,5] into n equal subintervals and using the right-hand endpoint for each c subscript k. Then take a limit of thissum as n-> infinite to calculate the area under the curve over [1,5].

Below you can see the problem. I was able to guess them correctly, so that I could perhaps try to work backwards to get it. Below is the problem. I found a. but i need to find parts b and c how do I do this?

Thanks,
MattView attachment 5501

 

[Greg]

Hi tornado711 and welcome to MHB!

It's not clear (at least to me) what you mean by "parts b and c". I don't see a reference to them anywhere on the attached image. Also, we ask (and our forum rules state) that users show their work, or any ideas on where to begin, when posting a problem. This eliminates the possibility of a redundant reply and gives us a clear idea of exactly what it is that you need help with. Can you post what you have done so far and clarify what you mean by "parts b and c"?