Find an expression for a sequence involving the sum of nth powers

[rugerts]

Homework Statement

a_n = 2*a_n-1 + a_n-2 -2*a_n-3.
a_0 = 5
a_1 = 18
a_2 = 14

Relevant Equations

No real equations. Shown below is a similar example done in class that I'm trying to base my solution around.

Example done in class:

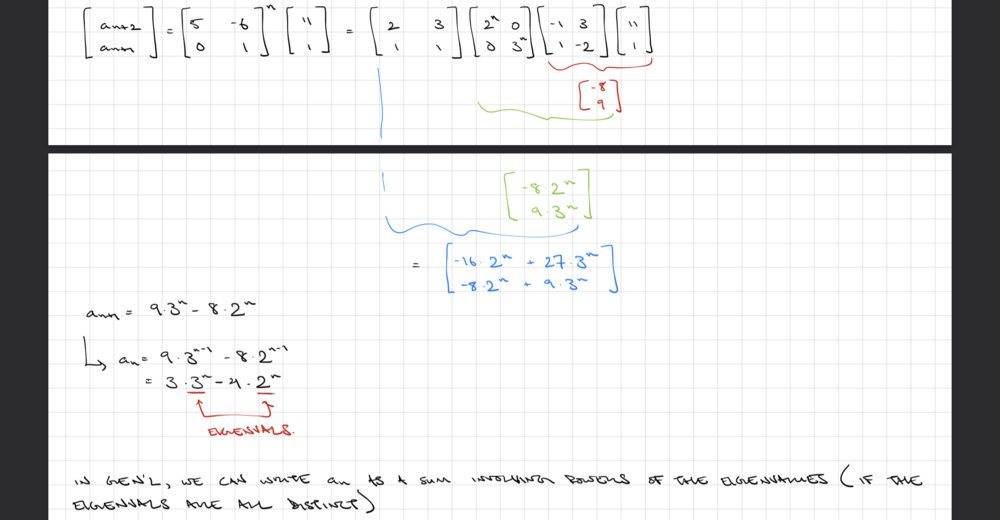The problem and my solution:

My solution seems incorrect because if I try to plug in 0, I don't get the initial condition given in the problem.

Does anyone see what I've done wrong along the way?

Thanks.

 

[mfb]

The equations would be much easier to read when typed here, with explanations what you do why.
$$a_n = \frac{5^n}{5} + \frac{7^n}{7} + \frac 2 3 3^n$$
You shouldn't get three different equations for a_n+1, a_n+2 and a_n+3.

Where do you plug in your initial conditions? You should have a general solution with three unknowns (which looks very different from what you got), these unknowns can be computed based on the initial conditions.

 

[rugerts]

The equations would be much easier to read when typed here, with explanations what you do why.
$$a_n = \frac{5^n}{5} + \frac{7^n}{7} + \frac 2 3 3^n$$
You shouldn't get three different equations for a_n+1, a_n+2 and a_n+3.

Where do you plug in your initial conditions? You should have a general solution with three unknowns (which looks very different from what you got), these unknowns can be computed based on the initial conditions.

Did you look through the first example I was shown in lecture? That general solution only has powers of n in it, which I think is the goal. Maybe I'm misunderstanding you.

 

[epenguin]

Not been through all your calculation, but I think you can do a quite simpler calculation in this case if you define a new variable, either
b_n = a_n - 2a_n-1
or probably better
c_n = a_n - a_n-2.

You then get a very simple series for the new variable, which you can convert into one, well maybe you should call it two, for the a_n .

 

[rugerts]

Not been through all your calculation, but I think you can do a quite simpler calculation in this case if you define a new variable, either
b_n = a_n - 2a_n-1
or probably better
c_n = a_n - a_n-2.

You then get a very simple series for the new variable, which you can convert into one, well maybe you should call it two, for the a_n .

Interesting. I hate to turn down simpler solutions but I think, since this is a course in linear algebra and we've just covered diagonalization, that we're expected to solve this using that technique.

 

[mfb]

Did you look through the first example I was shown in lecture? That general solution only has powers of n in it, which I think is the goal. Maybe I'm misunderstanding you.

If you consider powers of 0 and -1 it will work...

 

[rugerts]

So I actually had a mistake in matrix multiplication. I've got the correct solution now. My approach was fine. Thanks all.