SUMMARY
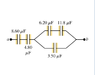
The discussion focuses on calculating the total energy stored in a capacitor network with a potential difference of 12.0 V. The energy stored in the network is derived using the formula U = 1/2 * C * V^2, where the equivalent capacitance is calculated from both series and parallel configurations of capacitors. The final energy stored in the 4.80 μF capacitor is determined to be 71.9 micro-J after correcting the calculations for charge and voltage across the capacitor.
PREREQUISITES
- Understanding of capacitor configurations (series and parallel)
- Familiarity with the energy storage formula for capacitors (U = 1/2 * C * V^2)
- Ability to calculate equivalent capacitance from multiple capacitors
- Basic knowledge of electrical charge (Q = C * V)
NEXT STEPS
- Study the principles of series and parallel capacitor combinations
- Learn how to derive equivalent capacitance for complex networks
- Explore energy calculations for capacitors in different configurations
- Investigate practical applications of capacitors in electronic circuits
USEFUL FOR
Students studying electrical engineering, electronics enthusiasts, and anyone looking to deepen their understanding of capacitor networks and energy storage calculations.