Find DFA Equiv: States, Transitions & Function

  • Context: MHB 
  • Thread starter Thread starter evinda
  • Start date Start date
  • Tags Tags
    Dfa Function States
Click For Summary

Discussion Overview

The discussion revolves around finding a deterministic finite automaton (DFA) equivalent to a given non-deterministic finite automaton (NFA). Participants explore the necessary states, transition functions, and the overall structure of the DFA, engaging in technical reasoning and clarification of rules.

Discussion Character

  • Technical explanation
  • Mathematical reasoning
  • Debate/contested

Main Points Raised

  • Some participants propose that the transition function should include the empty set as a state.
  • There is a discussion about the initial state of the DFA, with some suggesting it should be $\{A\}$.
  • Participants present a transition function and question whether it correctly represents the DFA.
  • Concerns are raised about missing transitions in the DFA, particularly from the state $\{A,B,C\}$.
  • Some participants discuss the reachability of states from the start state and whether unreachable states should be included in the DFA.
  • There is a debate about the necessity of including all states in the DFA, with some arguing that unreachable states can be omitted.
  • Participants analyze specific transitions, questioning the outcomes based on the defined rules.
  • Clarifications are made regarding the transitions from states based on input symbols.

Areas of Agreement / Disagreement

Participants generally agree on the need to include certain states and transitions, but there are multiple competing views regarding the inclusion of unreachable states and the correctness of specific transition functions. The discussion remains unresolved on some points.

Contextual Notes

Participants express uncertainty about the definitions and rules governing the construction of the DFA, particularly regarding reachable states and the completeness of the transition function.

evinda
Gold Member
MHB
Messages
3,741
Reaction score
0
Hello! (Wave)

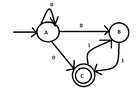
I want to find a DFA equivalent with the following:

View attachment 5867

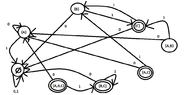
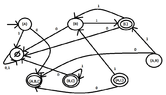
Do we have to follow the following procedure?

View attachment 5868

If so do we have to find the transition function having the following states?

$$\{A\} , \{ B \}, \{ C \}, \{ A,B \}, \{ A,C \}, \{ B,C \}, \{A,B,C\}$$
 

Attachments

  • dfa2.png
    dfa2.png
    2.8 KB · Views: 131
  • R.JPG
    R.JPG
    37.3 KB · Views: 106
Physics news on Phys.org
evinda said:
Hello! (Wave)

I want to find a DFA equivalent with the following:
Do we have to follow the following procedure?
If so do we have to find the transition function having the following states?

$$\{A\} , \{ B \}, \{ C \}, \{ A,B \}, \{ A,C \}, \{ B,C \}, \{A,B,C\}$$

Hey evinda! (Smile)

Yep, except that we should include $\varnothing$ as well. (Nerd)
 
I found the following transition function:

$$\delta': \begin{matrix}
& 0 & 1\\
\{A\} & \{A\} & \varnothing \\
\{B\} & \varnothing & \{C\}\\
\{C\} & \varnothing & \{B\}\\
\{A,B\} & \{A\} & \{C\}\\
\{A,C\} & \{A\} &\{B\} \\
\{B,C\} & \varnothing & \{B,C\}\\
\{A,B,C\} & \{A\} & \{B,C\}\\
\varnothing & \varnothing & \varnothing
\end{matrix}$$So the dfa will look as follows, right? (Thinking)View attachment 5872
 

Attachments

  • dfa3.png
    dfa3.png
    10.1 KB · Views: 127
evinda said:
I found the following transition function:

$$\delta': \begin{matrix}
& 0 & 1\\
\{A\} & \{A\} & \varnothing \\
\{B\} & \varnothing & \{C\}\\
\{C\} & \varnothing & \{B\}\\
\{A,B\} & \{A\} & \{C\}\\
\{A,C\} & \{A\} &\{B\} \\
\{B,C\} & \varnothing & \{B,C\}\\
\{A,B,C\} & \{A\} & \{B,C\}\\
\varnothing & \varnothing & \varnothing
\end{matrix}$$So the dfa will look as follows, right? (Thinking)

Hmm... the start state is missing... shouldn't we start with $q_0'=\{A\}$ as start state (rule 3)? (Wondering)

According to rule 2, shouldn't we have:
$$\delta'(q_0', 0) = \delta'(\{A\}, 0) = \bigcup_{r \in \{A\}} \delta(r, 0) = \delta(A,0) = \{A,B,C\}$$
(Wondering)
 
I like Serena said:
Hmm... the start state is missing... shouldn't we start with $q_0'=\{A\}$ as start state (rule 3)? (Wondering)

According to rule 2, shouldn't we have:
$$\delta'(q_0', 0) = \delta'(\{A\}, 0) = \bigcup_{r \in \{A\}} \delta(r, 0) = \delta(A,0) = \{A,B,C\}$$
(Wondering)

Oh yes, that's right! (Nod) Is everything else correct?
 
evinda said:
Oh yes, that's right! (Nod) Is everything else correct?

Well... we have indeed $\delta'(\{A\}, 1)=\varnothing$. (Nod)

But what should $\delta'(\{A,B,C\}, 0)$ be?
And $\delta'(\{A,B,C\}, 1)$? (Wondering)
 
I like Serena said:
Well... we have indeed $\delta'(\{A\}, 1)=\varnothing$. (Nod)

But what should $\delta'(\{A,B,C\}, 0)$ be?

$\{A,B,C \}$

I like Serena said:
And $\delta'(\{A,B,C\}, 1)$? (Wondering)

$\{B,C\}$

Right?
 
evinda said:
$\{A,B,C \}$

$\{B,C\}$

Right?

Right.

And isn't $\delta'(\{A,B\}, 0) = \{A,B\}$ and $\delta'(\{A,C\}, 0) = \{A,C\}$? (Wondering)
 
I like Serena said:
Right.

And isn't $\delta'(\{A,B\}, 0) = \{A,B\}$ and $\delta'(\{A,C\}, 0) = \{A,C\}$? (Wondering)

Isn't it $\delta'(\{A,B\}, 0) = \{A,B, C\}$ and $\delta'(\{A,C\}, 0) = \{A,B, C\}$ because of the transitions from A to C by reading 0 and from A to B by reading 0 respectively? Or am I wrong?
 
  • #10
evinda said:
Isn't it $\delta'(\{A,B\}, 0) = \{A,B, C\}$ and $\delta'(\{A,C\}, 0) = \{A,B, C\}$ because of the transitions from A to C by reading 0 and from A to B by reading 0 respectively? Or am I wrong?

Oh yes. You are right! (Blush)
 
  • #11

Attachments

  • ddfa.png
    ddfa.png
    8.9 KB · Views: 131
  • #12
evinda said:
So we get the following dfa, right?

I think there are 2 arrows missing from $\{A,B,C\}$... (Thinking)

Btw, did you notice that 4 of those 8 states are not reachable from the start state? (Wondering)
 
  • #13
I like Serena said:
I think there are 2 arrows missing from $\{A,B,C\}$... (Thinking)

Oh yes, right... I forgot to write the transition from $\{A,B,C\}$ to $\{A,B,C\}$ by reading 0, and the transition from $\{A,B,C\}$ to $\{B,C\}$ by reading 1.

So the dfa is the following:

View attachment 5881

I like Serena said:
Btw, did you notice that 4 of those 8 states are not reachable from the start state? (Wondering)
Yes, the states $\{ B \}, \{C\}, \{A,B\}, \{A,C\}$. :eek:
But all the states of a dfa should be reachable from the start state, right? (Thinking)
 

Attachments

  • ddfa.png
    ddfa.png
    9.1 KB · Views: 121
  • #14
evinda said:
Oh yes, right... I forgot to write the transition from $\{A,B,C\}$ to $\{A,B,C\}$ by reading 0, and the transition from $\{A,B,C\}$ to $\{B,C\}$ by reading 1.

So the dfa is the following:

Yep. (Nod)

Yes, the states $\{ B \}, \{C\}, \{A,B\}, \{A,C\}$. :eek:
But all the states of a dfa should be reachable from the start state, right? (Thinking)

Does the definition require that?
Last time I checked we can have unreachable states - it's just that we might as well leave them out.
They're just making the diagram messier than it needs to be. (Emo)
Anyway, the procedure you quoted did include all of them.
That is, it specifically said that the set of states would be $q'=\mathcal P(q)$.
 
  • #15
I like Serena said:
Last time I checked we can have unreachable states - it's just that we might as well leave them out.
They're just making the diagram messier than it needs to be. (Emo)

So a dfa equivalent to the given initial nfa is the following, right?View attachment 5882

In order to know which states are reachable from the starting state do we look at the states where we can go from the states where the starting state can go? (Blush)

I.e. in this case, we have

$\begin{matrix}
& 0 & 1\\
\{A\} &\{A,B,C\} & \varnothing
\end{matrix}$

and

$\begin{matrix}
& 0 & 1\\
\{A,B,C\} &\{A,B,C\} & \{B,C\}
\end{matrix}$

so we deduce that we have to include at the dfa the states $\{A\}, \{A,B,C\}$ and $\{B,C \}$, right? (Thinking)
 

Attachments

  • ddfa.png
    ddfa.png
    4.5 KB · Views: 109
  • #16
evinda said:
So a dfa equivalent to the given initial nfa is the following, right?

In order to know which states are reachable from the starting state do we look at the states where we can go from the states where the starting state can go? (Blush)

I.e. in this case, we have

$\begin{matrix}
& 0 & 1\\
\{A\} &\{A,B,C\} & \varnothing
\end{matrix}$

and

$\begin{matrix}
& 0 & 1\\
\{A,B,C\} &\{A,B,C\} & \{B,C\}
\end{matrix}$

so we deduce that we have to include at the dfa the states $\{A\}, \{A,B,C\}$ and $\{B,C \}$, right? (Thinking)

Yep. (Nod)

That leaves only to check where we can go from $\{B,C \}$. (Sun)
 
  • #17
I like Serena said:
Yep. (Nod)

That leaves only to check where we can go from $\{B,C \}$. (Sun)

I got it... Thanks a lot! (Smirk)
 

Similar threads

MHB What is the General Form of the Language Recognized by the Given Automaton?
  • · Replies 2 ·
Replies
2
Views
2K
MHB Proving Regularity of $L^R$ Using DFA Construction
  • · Replies 18 ·
Replies
18
Views
3K
Undergrad Discriminant function analysis - stepwise or otherwise?
  • · Replies 7 ·
Replies
7
Views
2K
MHB What Language Does This DFA Recognize?
  • · Replies 10 ·
Replies
10
Views
3K
MHB Finding DFA: Hint to Construct NFA for ((0∪1)*10* ∪ 0)
  • · Replies 43 ·
2
Replies
43
Views
8K
MHB What are the DFA configurations for L={w:${n}_{a}$(w) mod3 < 1} on $\sum$={a,b}?
  • · Replies 2 ·
Replies
2
Views
2K
MHB Creating DFA's for $\Sigma=\{0,1\}$ Languages
  • · Replies 4 ·
Replies
4
Views
2K
What are the differences between DFA's and FSM's?
  • · Replies 1 ·
Replies
1
Views
2K
MHB Satisfying S∘S=S: What Are The Conditions?
  • · Replies 7 ·
Replies
7
Views
2K
MHB Proving L is not Regular using Pumping Lemma
  • · Replies 1 ·
Replies
1
Views
2K