How can I accurately calculate distance using sound and various variables?

[L1988]

Two questions:
1. A sailor strikes the side of his ship just below the waterline. He hears the echo of the sound reflected from the ocean floor directly below 2.02 s later. How deep is the ocean at this point?

I assumed this used distance = speed x time. I knew that speed must equal the speed of sound in water, which I think is 1500 m/s (pretty sure, but not 100%) and I also divided my final distance by 2 so that I only got the distance of depth one way. However, the computer (this is online homework) said I was wrong, so I'm not sure where I went wrong. Any help would probably help me with the next problem too.


2.
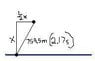
A rescue plane flies horizontally at a constant speed searching for a disabled boat. When the plane is directly above the boat, the boat's crew blows a loud horn. By the time the plane's sound detector perceives the horn's sound, the plane has traveled a distance equal to one half its altitude above the ocean. If it takes the sound 2.17 s to reach the plane, determine the altitude of the plane. Take the speed of sound to be 350 m/s.

Just like last time, I assumed that I should use

distance= speed of sound x time

with a new speed (350 m/s), new time, and this time distance doesn't have to be divided by 2. However, that got me the wrong answer.

Then I tried drawing a triangle, (since the plane has moved) and called my final distance r^2 and my x^2 = one half its altitude, so all that was left was y^2. This also was incorrect.

Where am I making a mistake?

 

[robertm]

1. Your reasoning and formulation is correct on this problem. I would suggest working it again and checking all your units, if it still marks it wrong I imagine the key is incorrect.


2. The key to this question does indeed involve triangles. And I am almost certain it has something to do with the fact that the plane makes a right triangle in which the short leg is one half the length of the long. But I can't for the life of me remember what that means. Hopefully this helps and I'm sure someone with a better memory will be along soon to help. for what its worth here's a sketch of how I picture the situation:
https://www.physicsforums.com/attachment.php?attachmentid=13740&stc=1&d=1209349520
rescue.jpg

 

[kalery]

On question 1, the sound waves travel to the ocean surface, then travel back to the boat.
Going down, gravity acts, which means you need an equation for constantly accelerating motion (y,yo,.5gt^2 etc).
Going up, you can apply the simple velocity equation t=d/v. Using this information in combination with the first equation and the information given, you can solve for "d".