Calculating Distance to a Wall Using Speed of Sound

[Barlock]

Homework Statement

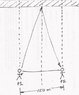
The human beings are standing at equal distances from a big and high wall. Distance between them is 150 m. When one fires the gun the other hears two shots in an interval of 2 seconds, using the speed of sound to be 340.298 m/s calculate their distance to the wall.

Homework Equations

V=x/t

The Attempt at a Solution

I don't know what two shots mean, i thought it means the sound is reflected from the wall, so i calculated time to reach girl 2 to girl 1 to be 0.44s subtractes from 2s and got 1.55s. Taking the time from guy1 to wall and wall to guy2 to be 1.55/2 i calculated distance to be 260m but that's not even close. What is wrong?

 

[dirk_mec1]

The second distance from the guy to the wall is calculated via pythagoras:

340.298=\frac{ \sqrt{ 150^2+x^2} }{(2-0.44)}

 

[insightful]

Draw a diagram of the wall and two people and really think about how the times and distances relate given the sound echoing off the wall.

 

[Barlock]

I got closer to the answer by writing that V*1.56=2x-V*0.44 but i get 340m which is less than true answer. My logic is this. It takes 0.44 s to get to guy 2 and by that time sound has traveled distance V*0.44 along x side of triangle whose base is 150 m. And third side is x...

 

[dirk_mec1]

Correction to my first post. I think this should do it: 340.298=\frac{ x+ \sqrt{ 150^2+x^2} }{(2-0.44)}

 

[insightful]

So, how much longer does the sound travel after the 0.44s toward the wall before the other guy hears the echo?

 

[dirk_mec1]

340.298=\frac{ x+ \sqrt{ 150^2+x^2} -150}{(2-0.44)}

 

[Barlock]

It travels for another 1.56 second the distance x + (x-V*0.44) right?

 

[insightful]

It travels for another 1.56 second the distance x + (x-V*0.44) right?

No. Re-read the problem. What is the time between the two sounds the other guy hears?

 

[dirk_mec1]

It travels for another 1.56 second the distance x + (x-V*0.44) right?

For sure the question is a posed vaguely. "In an interval of 2 seconds" can different interpretations.

Look at the dashed lines:

O    <--150m-->   O
|             /
|         /
|    /
|/______________ wall

 

[insightful]

When one fires the gun the other hears two shots in an interval of 2 seconds

To me, this clearly means that 2 seconds elapse between the two sounds. But, given the possible confusion, I'll just give my answer: 408.5m, and we'll see if this is what the author of the problem intended.

 

[dirk_mec1]

I disagree. It would've been clearer it the statement was like this:

When one fires the gun the other hears two shots in an interval of 2 seconds between the shots.

I get 401.76 m by the way.

 

[Barlock]

I have the same equation as you do but with a denominator being 2 rather than (2-0.44). I took it as 2 seconds between the shots. The answer book gives is 406 and i get 410.

 

[insightful]

For sure the question is a posed vaguely. "In an interval of 2 seconds" can different interpretations.

Look at the dashed lines:

O    <--150m-->   O
|             /
|         /
|    /
|/______________ wall

I can't tell if your sketch accurately indicates that the sound will echo from the mid-point on the wall between the men.

 

[Barlock]

Im sure the equation V=((x-150)+(150^2+x^2)^1:2)/2 accuretly describes the problem if its ment that 2 sec is the time between shots and 1.56 if its total time from begg of shot 1 to end of echo.

 

[insightful]

Im sure the equation V=((x-150)+(150^2+x^2)^1:2)/2 accuretly describes the problem if its ment that 2 sec is the time between shots and 1.56 if its total time from begg of shot 1 to end of echo.

Then solve for x (again) and see what you get.

 

[Barlock]

I get the answer 412, which is correct.

 

[insightful]

I get the answer 412, which is correct.

When I put 412 into your equation:

V = [(x-150)+(150^2+x^2)^1/2]/2

I get V = 350, not 340?

 

[Barlock]

Its 402 not 412 sorry, i rounded up wrong but the book tells its 412, so i guess they got it wrong.

 

[insightful]

Its 402 not 412 sorry, i rounded up wrong but the book tells its 412, so i guess they got it wrong.

Well, at least you've learned to always check your work by plugging your answer back into the equation.

You don't appear to be using the fact that the sound will echo off the wall at the mid-point between the men.

 

[Barlock]

What do you mean at the midpoint between the men? I think that the sound wave as it leaves the gun expands and hits the wall echoing back first again heard by guy who fired the gun as the circle of sound goes straight from gim to wall and back and the other catches the vibration only when the arch that's already met with guy 1 reaches guy 2. I imagine it being like that. What role does the mid point play?

 

[insightful]

What role does the mid point play?

A propagating wave, like sound, will reach its receiver in the shortest possible time (at constant velocity, this is also the shortest distance). The first sound is the sound traveling straight between the men. The second sound that echoes off the wall will first be heard after traveling the shortest possible distance between the men which includes bouncing off the wall. This shortest distance is bouncing off the wall at a point midway between the men, just as if one man threw a tennis ball to the other by bouncing it off the wall. Think of a beam of light reflecting off a mirror.

 

[insightful]

What role does the mid point play?

If you don't believe me:

http://hyperphysics.phy-astr.gsu.edu/hbase/sound/reflec.html

;-]

 

[Barlock]

Could you perhaps make some sorth of a drawing or a picture on how this represents the problem?

 

[insightful]

Could you perhaps make some sorth of a drawing or a picture on how this represents the problem?

Try this.

 

[dirk_mec1]

To me, this clearly means that 2 seconds elapse between the two sounds. But, given the possible confusion, I'll just give my answer: 408.5m, and we'll see if this is what the author of the problem intended.

Your answer is not agreeing with the answer book...

 

[insightful]

I've seen 406m and 412m; which does the book say?

 

[dirk_mec1]

Barlock, what is the answer your book gives to this question? I agree with Insightful by the way the soundwave will bounce in the midpoint.

 

[Barlock]

It appears that the answer book i have says its 406, while the paper i got says 412. I guess someone done it wrong on paper, but the book must be correct so its 406. When i do the midpoint thing i get the equation V=x-75 and y being the shortest distance to wall is (x^2-75^2)^1/2 which gives me approximately 408.9.

 

[dirk_mec1]

I get 408.46 m but your answer is probably okay due to some rounding. Unless I've missed something I guess the answer book is incorrect.

Maybe Insightful has something to add?

 

[insightful]

My work here is done.

;-]

 

[dirk_mec1]

Ok, Barlock, the concusion is that the answer in the book is incorrect!