Find Elevation at Point A - Math Homework
- Thread starter MrMechanic
- Start date
Click For Summary
SUMMARY
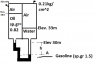
The discussion revolves around calculating the elevation at point A in a fluid mechanics problem involving two tanks connected by a pipe. The participants utilize the equation P = pgh, converting pressures from kg/cm² to kN/m² and discussing specific gravity in relation to density. Key calculations include determining pressures at various heights and addressing the significance of specific gravity and density in the equations. The final calculations lead to a height (h) of approximately 5.235 meters based on the pressure equilibrium principle.
PREREQUISITES- Understanding of fluid mechanics principles, specifically hydrostatic pressure.
- Familiarity with the equation P = pgh and its application in pressure calculations.
- Knowledge of specific gravity and its relationship to density.
- Ability to convert units between kg/cm² and kN/m².
- Learn about hydrostatic pressure calculations in fluid mechanics.
- Study the concept of specific gravity and its implications in fluid density.
- Explore unit conversions in fluid mechanics, particularly between different pressure units.
- Investigate the principles of pressure equilibrium in connected fluid systems.
Students and professionals in engineering, particularly those studying fluid mechanics, as well as anyone involved in solving practical problems related to pressure and elevation in fluid systems.
Similar threads
- · Replies 12 ·
- · Replies 3 ·
- · Replies 3 ·
- · Replies 9 ·
- · Replies 5 ·
- · Replies 8 ·