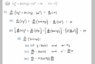Find eqn of Tangent Line to graph- Implicit Differentiation

[opus]

Homework Statement

Find the equation of the tangent line to the graph of the given equation at the indicated point.

$xy^2+sin(πy)-2x^2=10$ at point $(2,-3)$

Homework Equations

The Attempt at a Solution

Please see attached image so you can see my thought process. I think it would make more sense that typing it out.
My solution is $\frac{7}{-12-π}$ But I don't think this is correct. The $πy$ inside the argument of the sin function is throwing me off.

 

[opus]

Image.

Let me add that I know this problem isn't finished. Up to my current position is where I'm seeking clarification.
Thanks!

 

[fresh_42]

I cannot read your image without further processing. The denominator looks o.k. but the nominator seems to be wrong. Your slope is roughly $-\frac{1}{2}$ whereas the plot looks more like $\pm 0$.

 

[opus]

Hopefully this makes it better. If not I’ll type it all out.
I’ve broken the image up into two pieces but since the steps are labeled, it should be clear in the order they are.

 

[fresh_42]

And what is $8-9$?

 

[opus]

That's embarrassing
So we have $\frac{-1}{-12-π}$ and this makes more sense now. So this is the slope of the tangent line at (2,-3) and now I can continue on hopefully without forgetting how to add.