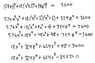SUMMARY
The discussion focuses on finding the equation of a surface defined by the vector-valued function G=(24xy, 12(x^2+2), 18z^2) where the magnitude |G| equals 60. The correct formulation involves calculating |G| as the square root of the sum of the squares of its components, leading to the equation |G| = √((24xy)² + (12(x² + 2))² + (18z²)²). The participants emphasize simplifying this expression and setting it equal to 3600 to eliminate the square root, which ultimately defines the surface in three-dimensional space.
PREREQUISITES
- Understanding of vector-valued functions
- Knowledge of calculating magnitudes of vectors
- Familiarity with algebraic manipulation and simplification
- Basic concepts of three-dimensional geometry
NEXT STEPS
- Study the properties of vector-valued functions in multivariable calculus
- Learn how to compute and interpret the magnitude of vectors
- Explore methods for simplifying algebraic expressions involving radicals
- Investigate the implications of points on surfaces in three-dimensional space
USEFUL FOR
Students in calculus and advanced mathematics, particularly those dealing with vector calculus and surface equations, as well as educators looking for examples of vector magnitude applications.