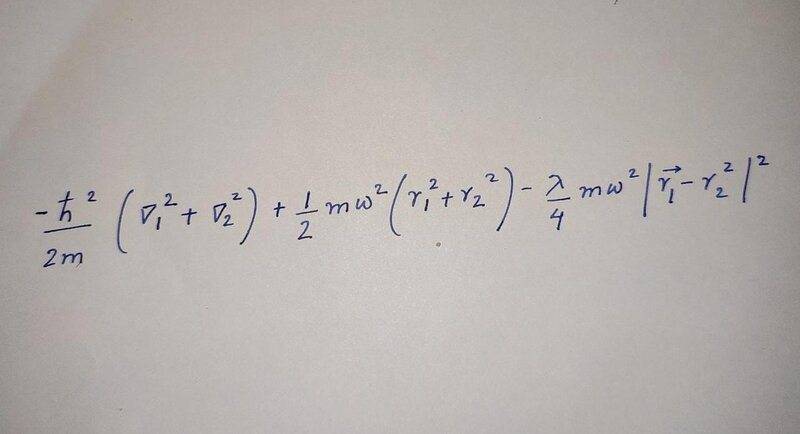SUMMARY
The discussion focuses on finding the exact ground state energy of the Hamiltonian for a 3D harmonic oscillator. Participants suggest rewriting the equation using new variables, specifically defining \(\vec{R} = \frac{1}{2} (\vec{r}_1 + \vec{r}_2)\) and \(\vec{r} = \vec{r}_1 - \vec{r}_2\). This substitution aims to separate the Hamiltonian into two distinct Hamiltonians, one dependent on the \(\vec{R}\) coordinate and the other on the \(\vec{r}\) coordinate. Clarifications regarding typographical errors in the equations were also requested to ensure accurate communication.
PREREQUISITES
- Understanding of Hamiltonian mechanics
- Familiarity with 3D harmonic oscillators
- Knowledge of vector notation in physics
- Basic skills in mathematical substitutions and transformations
NEXT STEPS
- Research Hamiltonian mechanics in quantum systems
- Study the properties of 3D harmonic oscillators
- Learn about variable transformations in quantum mechanics
- Explore methods for separating variables in Hamiltonians
USEFUL FOR
Physicists, graduate students in quantum mechanics, and researchers working on harmonic oscillator models will benefit from this discussion.