Find Point on Rect Inside Circle Given Angle

[Norpyx]

Alright, this is a bit of a confusing one for me.

The problem:

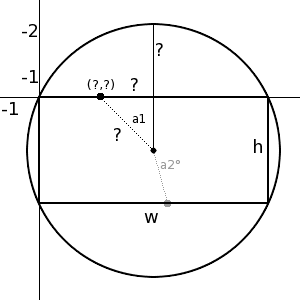
The ultimate objective is to get the coordinates of the points on the edge of the rectangle (labeled: (?,?) ), given the angle, and the height and width of the rectangle.

The more I think about this problem, however, the more I confuse myself. Before I was going to outline some steps I thought I needed to take to get that point (and ask for the equations) but now I'm not sure what I need to do anymore.I want to highlight that I know the height and width of the rectangle, and the angle.

I know I can find the distance between the center dot by dividing the height or width by two, depending on what axis, since its the point in the center of the rectangle.

Any help at all?

 

[Tinyboss]

You've got a right triangle there. You know an angle a1 and an adjacent side (it's h/2). Use trigonometry to find the opposite side.

 

[Norpyx]

The problem is, as you see with the faded a2 angle (which would also be known), the angle isn't always less than or equal to 90 degrees.

I've wrapped my head around the concept a bit more, so I'll post up a more relevant question/example in a second.

The above is a better example of exactly what I need to do.

Known variables: h, w, a, b, c1, d1, e1, f1, and z.
Unknown variables: c2, d2, e2, f2, m, and n

I need to find m,n and then translate c1,d1 to c2,d2 and the same for e1,f1 to e2,f2. Originally I was going to do the translation and what not myself, but its easier to explain the entire problem in one go.

 

[Norpyx]

New Data!

Given the fact that all corner points of the rectangle are points on the circle's circumference, we can find the diameter by calculating the distance between two opposite corners of the rectangle.

For example, if the width of the rectangle was 1280, and the height was 960, then the circle's diameter is 1600, making the radius 800.

sqrt( (1280-0)^2 + (960-0)^2 )

Now, is it possible to find the distance between the point on the rectangle and the center of the circle, since the angle will be the same, and we can find the point on the circle's circumference, now that we have the diameter?