Find speed of CoM after collision between ball and "square structure"

[songoku]

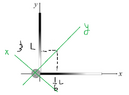
Homework Statement

Please see below

Relevant Equations

$\bar x=\frac{1}{M}\int_{a}^{b}x\lambda(x)dx$
$L=I\omega$
$L=r\times p$
Conservation of linear momentum
Conservation of angular momentum

(a)
$$\bar x=\frac{\int_{0}^{L} \frac{\alpha_o}{L}x^2dx}{\int_{0}^{L}\frac{\alpha_o}{L}xdx}$$
$$=\frac{2}{3}L$$

(b)
$$x=\frac{x_1+x_2}{2}=\frac{1}{6}L$$

$$y=\frac{y_1+y_2}{2}=\frac{1}{3}L$$

(c) I am not sure about this part. Do I need to divide the conservation of momentum into two directions?

In x-direction:
$$M.v_o\sin\theta=3M.v_{f,CM}x$$
$$v_{f,CM}x=\frac{2\sqrt{5}}{15}v_o$$

In y-direction:
$$M.v_o\cos\theta=3M.v_{f,CM}y$$
$$v_{f,CM}y=\frac{\sqrt{5}}{15}v_o$$

So:
$$v_{f,CM}=\sqrt{(v_{f,CM}x)^2+(v_{f,CM}y)^2}$$
$$=\frac{1}{3}v_o$$

Is that correct?

Thanks

 

[kuruman]

(c) I am not sure about this part. Do I need to divide the conservation of momentum into two directions?

Conservation of what kind of momentum in two directions?
The linear momentum of the CM of the system consisting of the two rod structure plus the particle is initially only in the x-direction. Momentum conservation means that it is the same after the collision, i.e. still only in the x-direction.

There is another kind of momentum that is conserved through the collision. What kind might that be? Hint: It's in a direction perpendicular to the xy-plane.

 

[haruspex]

Momentum conservation means that it is the same after the collision, i.e. still only in the x-direction.

Except that there will be a vertical impulse from the table.

 

[songoku]

Except that there will be a vertical impulse from the table.

Why is there vertical impulse from the table?

Conservation of what kind of momentum in two directions?
The linear momentum of the CM of the system consisting of the two rod structure plus the particle is initially only in the x-direction. Momentum conservation means that it is the same after the collision, i.e. still only in the x-direction.

Conservation of linear momentum, because I thought there is no net external force acting on the system (particle and L-rod) so the linear momentum should be conserved but based on hint from @haruspex there would be vertical impulse so linear momentum won't be conserved.

There is another kind of momentum that is conserved through the collision. What kind might that be? Hint: It's in a direction perpendicular to the xy-plane.

I suppose conservation of angular momentum can be applied to point (0, 0).

I think maybe during the collision there will be force acting on L-rod to the right, causing it to rotate counterclockwise.

$$L_{initial}=L_{final} ~\text{at origin}$$
$$0=r\times p+I\omega$$

Am I even on the right direction?

Thanks

 

[kuruman]

Except that there will be a vertical impulse from the table.

I read the problem to mean that the plane of the L-shaped structure is parallel to the (frictionless) table. I interpreted the figure to be a top view of the structure resting on the table. The statement "The square structure then rests along the x-axis on a frictionless, horizontal table" says nothing about the y-direction being along the vertical.

I think maybe during the collision there will be force acting on L-rod to the right, causing it to rotate counterclockwise.

You mean that there is a torque exerted by the particle on the L-shaped structure to cause the counterclockwise rotation. Where do you think the axis of this rotation will be?

 

[songoku]

You mean that there is a torque exerted by the particle on the L-shaped structure to cause the counterclockwise rotation. Where do you think the axis of this rotation will be?

I think the particle will rotate about the center of mass of the whole system.

I already have the CM of the L-rod, which is $\left(\frac{1}{6}L, \frac{1}{3}L\right)$. Adding the particle of mass $M$ will change the CM of the system to $\left(\frac{1}{18}L, \frac{1}{9}L\right)$

The final CM is supposed to be the axis of rotation

 

[haruspex]

I read the problem to mean that the plane of the L-shaped structure is parallel to the (frictionless) table. I interpreted the figure to be a top view of the structure resting on the table.

You are probably right. I read "rests along the x axis" as meaning it only rests on that. Otherwise, why not say it rests along the x and y axes?
Also, if it is lying flat on the table, doesn’t question c become trivial (and @songoku's answer correct, but done very much the hard way)?

 

[songoku]

Also, if it is lying flat on the table, doesn’t question c become trivial (and @songoku's answer correct, but done very much the hard way)?

I just realized I got the same answer by doing simple calculation:
$$M.V_o=3M.v_{f,CM}$$
$$v_{f,CM}=\frac{1}{3}v_o$$

My first thought was I need to consider the collision where the CM of particle and CM of L-rod are in one line, that's why I divide the working in two directions but apparently it is not needed. So conservation of momentum can be applied even though the CM of two objects are not in a straight line?

And if let say the case is the plane of L-rod is perpendicular to the table, why is there vertical impulse from the table?

I imagine the L-rod will still rotate counterclockwise due to the force exerted by the particle during collision. Is the rotation causing the vertical impulse?

 

[haruspex]

Is the rotation causing the vertical impulse?

Yes. If this were in the absence of gravity and no table then the rotation would cause the junction of the two rods to move into the negative y half of the plane. To avoid being penetrated, the table exerts a vertically upward impulse.

 

[songoku]

Yes. If this were in the absence of gravity and no table then the rotation would cause the junction of the two rods to move into the negative y half of the plane. To avoid being penetrated, the table exerts a vertically upward impulse.

If there is no particle hitting the L-rod, the table also exerts a vertical force on the rod, which is normal force, and the magnitude is equal to the weight of the rod.

After being hit, is the vertical force from the table equal to weight of particle + weight of L-rod?

 

[haruspex]

After being hit, is the vertical force from the table equal to weight of particle + weight of L-rod?

There is an impulse, just as the particle exerts an impulse on the rods. Don’t think of it as a force since that will be of unknown magnitude and duration. In the idealisation it is an unbounded force acting for an infinitesimal time. Consequently, gravity is irrelevant during the impulse.

 

[songoku]

There is an impulse, just as the particle exerts an impulse on the rods. Don’t think of it as a force since that will be of unknown magnitude and duration. In the idealisation it is an unbounded force acting for an infinitesimal time. Consequently, gravity is irrelevant during the impulse.

Is my method in post #4 correct?

 

[kuruman]

You are probably right. I read "rests along the x axis" as meaning it only rests on that. Otherwise, why not say it rests along the x and y axes?

Good question.

Also, if it is lying flat on the table, doesn’t question c become trivial . . .

It does for the expert but not for the novice. I think there is educational value here. In linear moment conservation problems the autopilot approach is to write $$\mathbf P_{\text{before}}=\mathbf P_{\text{after}}$$, find expressions for each side of the equation in terms of the velocities of the moving parts and solve for what is asked. The origin $$\Delta (\mathbf V_{\text{CM}}) =0$$ of this equation is forgotten as we can see from @songoku's convoluted, but correct, answer for the velocity of the CM.

To @songoku:
Linear momentum conservation means that the the linear velocity of the CM of the three-mass isolated system does not change: if you know it at one point in time, you know it at all points in time. Here, before the collision, you have mass $M$ moving with velocity $\mathbf v_0$ and two masses $M$ each at rest. The momentum of the CM before the collision is $$\mathbf V_{\text{CM}}=\frac{M \mathbf v_0+M*0+M*0}{M+M+M}=\frac{1}{3}\mathbf v_0.$$ Since this velocity doesn't change, it has the same value after the collision. It's as simple as that.

 

[kuruman]

Is my method in post #4 correct?

The method to reach what goal? Please specify your goal and what the symbols in the equations stand for.

 

[Lnewqban]

My first thought was I need to consider the collision where the CM of particle and CM of L-rod are in one line,

But the movement direction of the colliding mass is not in line with the CM of the pre-collision L-shaped rod.

Because of the above, the non-elastic collision should induce simultaneous rotation and translation of the newly formed three-mass system respect to the flat horizontal frictionless surface.

 

[kuruman]

But the movement direction of the colliding mass is not in line with the CM of the pre-collision L-shaped rod.

It doesn't have to be. Since there is no external torque on the L-shaped structure + particle system, the angular momentum about any point is conserved. In this problem, one would choose the CM of the system as the reference for angular momentum because this simplifies the conservation equation to $$Mv_0~d=I\omega$$ where $~d=~$distance of the CM to the x-axis; $I=~$moment of inertia of the composite object after the collision about its CM. In this form, there is only orbital angular momentum before the collision and only spin angular momentum after the collision. OP's choice was to start with zero angular momentum effectively moving the orbital part from the left hand side to the right hand side.

 

[songoku]

The method to reach what goal? Please specify your goal and what the symbols in the equations stand for.

I want to find the speed of CM of the system $(v_{f,CM})$ for the case considered by @haruspex scenario.

The coordinate of CM of L-rod is $\left(\frac{1}{6}L,\frac{1}{3}L\right)$ and after adding the particle, the CM becomes $\left(\frac{1}{18}L,\frac{1}{9}L\right)$

I am taking $\left(\frac{1}{18}L,\frac{1}{9}L\right)$ as the location of axis of rotation.

Consider the conservation of angular momentum:
$$\text{total initial angular momentum}=\text{total final angular momentum}$$
$$M.v_0.\frac{1}{9}L=(I_{particle}+I_{L-rod})\omega...(1)$$

Next, my idea is:
a) Find the moment of inertia of one rod using $I=\int_{0}^{L}r^2 dm$, taking the axis of rotation at origin, then using parallel axis theorem, I move the axis of rotation to $\left(\frac{1}{18}L,\frac{1}{9}L\right)$

b) Solve equation (1) for $\omega$

c) Use conservation of kinetic energy to find $v_{f, CM}$
$$\frac{1}{2}M(v_0)^2=\frac{1}{2}.3M.(v_{f,CM})^2+\frac{1}{2}.(I_{particle}+I_{L-rod})\omega^2$$

Is my approach correct?

 

[erobz]

c) Use conservation of kinetic energy to find $v_{f, CM}$
$$\frac{1}{2}M(v_0)^2=\frac{1}{2}.3M.(v_{f,CM})^2+\frac{1}{2}.(I_{particle}+I_{L-rod})\omega^2$$

Is my approach correct?

Isn't the ball sticking to the "L" structure? Meaning it experiences a certain amount of plastic deformation (perfectly inelastic collision)?

BTW does anyone see the optical illusion with the rods? To me it appears as though the lines are not everywhere parallel because of that gradient.

 

[haruspex]

I am taking $\left(\frac{1}{18}L,\frac{1}{9}L\right)$ as the location of axis of rotation.

That would not produce the correct motion for the point where the rods meet. We know that must move horizontally.
I would take the motion as the sum of the linear motion of that point and a rotation about it.

Consider the conservation of angular momentum:

With angular motion you need to specify the axis you are using. For the angular momentum to be conserved there must be no external impulse about that axis.
And to avoid pitfalls, it is best to choose an axis fixed in space, not fixed in the moving body.
Since we expect there to be an impulse from the table, that means you should choose the point (0,0).

c) Use conservation of kinetic energy

As @erobz notes, KE is not conserved here.

 

[kuruman]

BTW does anyone see the optical illusion with the rods? To me it appears as though the lines are not everywhere parallel because of that gradient.

The look parallel to me.

 

[erobz]

The look parallel to me.

View attachment 354172

I meant with the image of a single rod. The rod appears like it gets wider at the white portion, and is kind of curved in the transition between black and gray. I know the lines are parallel after putting a ruler up to the screen, but I think my brain/eyes system are not sure of it.

Its not related to the problem, just seeing if others see the apparent optical illusion.

 

[haruspex]

I meant with the image of a single rod. The rod appears like it gets wider at the white portion, and is kind of curved in the transition between black and gray.

Yes, I see that. I believe it is an example of "Helmholtz irradiation".

 

[kuruman]

Yes, I see that. I believe it is an example of "Helmholtz irradiation".

Oh that. My wife calls it the "you-look-slimmer-in-dark-clothes" illusion.

 

[Lnewqban]

In this form, there is only orbital angular momentum before the collision and only spin angular momentum after the collision.

Sorry @kuruman, I don't understand the concepts of orbital angular momentum and spin angular momentum.
Could you please explain those a little more?

 

[songoku]

That would not produce the correct motion for the point where the rods meet. We know that must move horizontally.
I would take the motion as the sum of the linear motion of that point and a rotation about it.

With angular motion you need to specify the axis you are using. For the angular momentum to be conserved there must be no external impulse about that axis.
And to avoid pitfalls, it is best to choose an axis fixed in space, not fixed in the moving body.
Since we expect there to be an impulse from the table, that means you should choose the point (0,0).

As @erobz notes, KE is not conserved here.

Taking (0,0) as axis of rotation:
$$0=-3M.v_{f,CM}.\frac{1}{9}L+(I_{L-rod})\omega$$

Then how to proceed? I have 2 unknowns

 

[haruspex]

I don't understand the concepts of orbital angular momentum and spin angular momentum.

The rotational motion of a body wrt an axis can be thought of as made up of a rotation of its mass centre about the axis (orbital angular momentum $=m\vec r\times\vec v$) plus a rotation of the body about its mass centre (spin angular momentum $=I\vec \omega$).

Taking (0,0) as axis of rotation:
$$0=-3M.v_{f,CM}.\frac{1}{9}L+(I_{L-rod})\omega$$

The mass centre will have an X component and a Y component of velocity.
I would represent the motion just after impact as a velocity of the particle and an angular velocity. Since the particle still has no rotation around (0,0) we can leave that out and just consider the angular momentum of the rods about (0,0). It might be simpler to calculate for each rod separately and sum them.

You also still have conservation of linear momentum in the X direction.

 

[kuruman]

Sorry @kuruman, I don't understand the concepts of orbital angular momentum and spin angular momentum.
Could you please explain those a little more?

Example
(a) Orbital angular momentum or angular momentum of the center of mass.
The Earth has orbital angular momentum about the center of the Sun given by $~\vec L_{\text{orb.}}=M_E \vec V_E \times \vec R_{SE}~$, where
$M_E=~$ mass of theEarth; $\vec V_E=$velocity of the Earth in its orbit; $\vec R_{SE}=$ Earth's position relative to the Sun. Note that one can write $\vec V_E=\vec{\Omega} \times \vec R_{SE}$ where $~\Omega =\dfrac{2\pi}{365.25}~\dfrac{\text{rad}}{\text{day}}~$ is the angular speed of the Earth in its orbit. Substituting, $$\vec L_{\text{orb.}}=M_E \vec V_E \times \vec R_{SE}=M_E (\vec{\Omega} \times \vec R_{SE}) \times \vec R_{SE}=M_ER_{SE}^2\vec {\Omega}.$$ The direction of $\vec \Omega$ is perpendicular to the plane of the orbit also known as the ecliptic. Note that one can also write $\vec L_{\text{orb.}}=I_{\text{orb.}}~\vec {\Omega}$ where $I_{\text{orb.}}=M_ER_{SE}^2$ is the moment of inertia of a point-mass Earth relative to the center of the Sun.

(b) Spin angular momentum or angular momentum about the center of mass.
As it orbits the Sun, the Earth also rotates about an axis that goes through its CM with an angular speed $~\omega =\dfrac{2\pi}{1}~\dfrac{\text{rad}}{\text{day}}.$ The spin angular momentum is $$\vec L_{\text{spin}}=I_{CM} \vec {\omega}.$$ Here $I_{\text{CM}}$ is the moment of inertia of the Earth about its axis of rotation. If we approximate the Earth as a smooth sphere, $I_{\text{CM}}=\frac{2}{5}M_E R_E^2.$ The direction $\vec {\omega}$ is along the Earth's axis of rotation which is tipped by 23.4° away from the perpendicular to the ecliptic.

Thus, the total angular momentum of the Earth is the vector sum of two terms, $$\vec L_{\text{total}}=M_ER_{SE}^2~\vec {\Omega}+\frac{2}{5}M_E R_E^2~\vec{\omega}.$$

 

[Lnewqban]

Thank you much, @haruspex and @kuruman