Find sum of all odd square numbers

  • #1
chwala
Gold Member
2,745
387
Homework Statement
see attached
Relevant Equations
sum of series.
There is a mistake on this textbook (The mistake is pretty obvious) but hey I hope I did not miss something...

ought to be ##40425 - 19600##

1712630951026.png
 
Physics news on Phys.org
  • #2
chwala said:
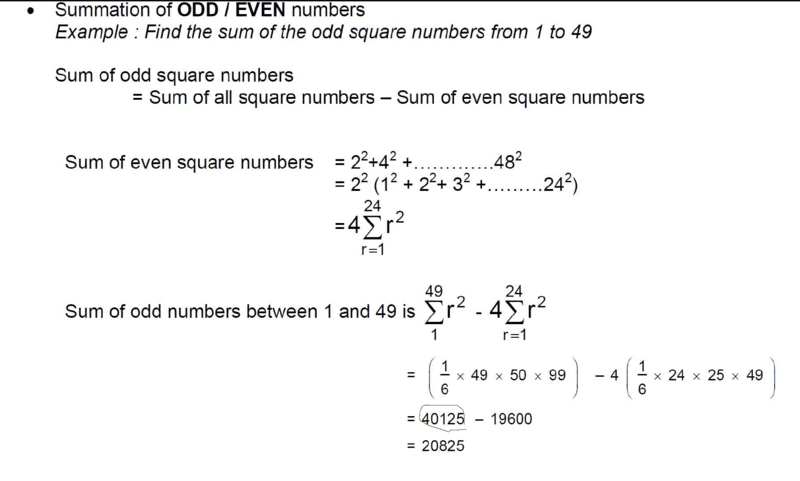
ought to be 40425
Agreed.
 
  • Like
Likes chwala

Similar threads

Finding the projection of a Vector
Replies
4
Views
929
What does the square of a differential mean?
Replies
2
Views
2K
Find the limit of the sum of the areas of all these triangles
Replies
7
Views
719
Finding the least possible sum of a product.
Replies
3
Views
4K
Proof in number theory: the sum of all divisors of n
Replies
12
Views
1K
Are Two Random Numbers More Likely to Have a Quotient Closer to an Odd Integer?
Replies
23
Views
1K
Understanding the Solution for Finding the Sum of Digits of m
Replies
3
Views
1K
Finding the relative extrema for a speed function using parametric curves
Replies
11
Views
2K
Geometric sum using complex numbers
Replies
4
Views
2K
Statistics: given total sum of squares, find R²
Replies
4
Views
2K

Hot Threads

Recent Insights

Back
Top