MHB Find Tangent Lines to Polar Graph: r=2-3sin(θ)

[MarkFL]

Here is the question:

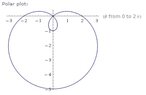
How do I find the polar coordinates for the horizontal and vertical tangent lines?

For r=2-3sin(θ)

With decimal approximations to 4 places for the angles at which the tangent lines occur?

I keep messing up when I try to do this on my own, much appreciation to any who help

I have posted a link there to this topic so the OP can see my work.

 

[MarkFL]

Hello Uncorrupted.Innocence,

The first thing I would do is look at a polar plot of the given function:

View attachment 1018

Next, let's parametrize the curve:

$$x=r\cos(\theta)=\left(2-3\sin(\theta) \right)\cos(\theta)$$

$$y=r\sin(\theta)=\left(2-3\sin(\theta) \right)\sin(\theta)$$

Hence:

$$\frac{dx}{d\theta}=\left(2-3\sin(\theta) \right)\left(-\sin(\theta) \right)+\left(-3\cos(\theta) \right)\cos(\theta)=6\sin^2(\theta)-2\sin(\theta)-3$$

Equating this to zero, and applying the quadratic formula, we find:

$$\theta=\sin^{-1}\left(\frac{1\pm\sqrt{19}}{6} \right)$$

Because $\sin(\pi-\theta)=\sin(\theta)$, we also have:

$$\theta=\pi-\sin^{-1}\left(\frac{1\pm\sqrt{19}}{6} \right)$$

We may add integral multiples of $2\pi$ as needed to place $0\le\theta<2\pi$.

So, rounded to four places, the angles at which the tangent lines are vertical are:

$$\theta\approx1.1043,\,2.0373,\,3.7358,\,5.689$$

$$\frac{dy}{d\theta}=\left(2-3\sin(\theta) \right)\left(\cos(\theta) \right)+\left(-3\cos(\theta) \right)\sin(\theta)=2\cos(\theta)\left(1-3\sin(\theta) \right)$$

Equating each factor in turn to zero, we find:

$$\cos(\theta)=0$$

$$\theta=\frac{\pi}{2},\,\frac{3\pi}{2}$$

$$1-3\sin(\theta)=0$$

$$\theta=\sin^{-1}\left(\frac{1}{3} \right),\,\pi-\sin^{-1}\left(\frac{1}{3} \right)$$

So, rounded to four places, the angles at which the tangent lines are horizontal are:

$$\theta\approx0.3398,\,1.5708,\,2.8016,\,4.7124$$