- #1
einsteinoid
- 42
- 0
Homework Statement
Find the total area of the region enclosed by the curve x = y2/3 and the lines x = y and y = -1.
2. The attempt at a solution
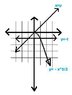
I graphed x = y2/3 as y=x3/2 and y=-x3/2. Then I graphed the lines y=x and y=-1.
I shaded the region in question, which appears off the cuff to have an area slightly larger than one. To find the area exactly I broke the problem up into two integration steps.
1. [tex]\int[/tex] x dx (from x=-1 to x=0) - [tex]\int[/tex] -1 dx (in the same range of x=-1 to x=0)
+
2. [tex]\int[/tex] -1 dx (from x=0 to x=1) - [tex]\int[/tex] -x3/2 dx
I keep getting the whole area as 11/10. This seems close enough, seeing as how the area appears to be slightly greater than 1. However, my textbook's answer glossary tells me that the correct answer is actually 6/5. Can anyone tell me what I'm doing wrong?
I attached a relevant graph (I did it in mspaint, lol, sorry). y=+x2/3 is left out of the graph because it is irrelevant. The shaded region, I'm assuming, is the area in question:
Attachments
Last edited: