Find the car's speed at point when deceleration is increased - Mechanics

[chwala]

Homework Statement

See attached

Relevant Equations

kinematics

Wawawawawawa! This was a tough one...

Find the question below;

Find my approach below:
We have the following equations;
1. $v=30-0.5t$
2. $v=30-1.5t$

Now the car changes its acceleration at some point i.e from $-\frac{1}{2}$ $m/s^2$ to $-\frac{3}{2}$ $m/s^2$ ...
I considered the following graphs for the two equations, assuming that the second equation was also starting from the point $v=30$$m/s$

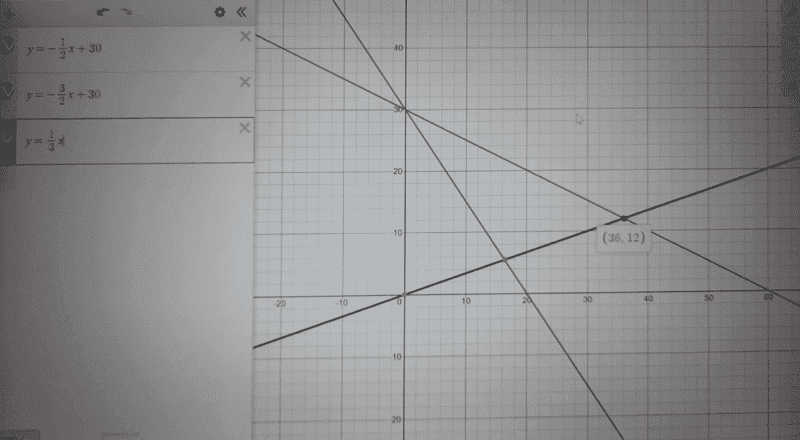
Now the graph of $v=30-1.5t$ will give us some perspective on how it relates to the graph of $v=30-0.5t$ at some point...noting that the desired graph will be parallel to $v=30-1.5t$.
Now i attempted to find the scale factor $m$ connecting the two functions by letting,
$-\frac{3}{2}$m = $-\frac{1}{2}$
$→m$= $\frac{1}{3}$ therefore plotting the graph,
$v$= $\frac{1}{3}t$ realizes the point that we were looking for where, $(t,v)$=$(36,12)$
Therefore, the speed of the car at the point where deceleration is increased is $12$ m/s and the time taken for the car to stop is given by
using $v=u +at$
$0$= $12$+ $-\frac{3}{2}$$t$
$t=8$, therefore time taken for car to stop is $36+8=44$seconds

bingo guys
There may be a better approach to what i have done...

 

[mjc123]

The answer is correct, but I don't get the logic here:

Now i attempted to find the scale factor m connecting the two functions by letting,
−3/2 m = −1/2
→m= 1/3 therefore plotting the graph,
v= 1/3 t realizes the point that we were looking for where, (t,v)=(36,12)

Why do you plot y = x/3?
You don't use the fact that you are given the total stopping distance. You could make the change in acceleration at any point during the first stage, and the stopping distance would be different. Did you get the right answer by coincidence?
I plotted a v-t graph and worked out the distance (area under the curve) as a function of T, the time at which the acceleration is changed, and solved the quadratic equation in T.

 

[chwala]

I plotted the graph $y$=$\frac {x}{3}$ to find the point where it intersects the graph, $y$=$\frac {-1}{2}$ $x$+$30$. By noting that the desired line would be parallel to the line $y$=$\frac {x}{3}$

 

[mjc123]

What is the "desired line"? Why is it parallel to y=x/3? There are an infinite number of lines parallel to y=x/3. Why that one in particular?

 

[Merlin3189]

I too was puzzled by the logic, even after I checked the result and found it correct. I have tried to follow the method for other situations, particularly where m1 = -0.5 and tried various values of m2 such as -1, -1.5, -2, -2.5 just to keep the sums easy for my poor old brain. It only seems to work for m2 = -1.5 and I'm still mystified as to how OP managed to hit on a rule that seems to work only in this particular situation. Did he know the answer and notice the convenient y=x/3 relation at the corner, then spot the rule?

BTW I'm also looking at his other post and am equally befuddled by his explanation of how he gets the right answer. Where the numbers in the √( ...) come from I just can't see. Clearer explanations are needed if we are to check the work.

 

[chwala]

I too was puzzled by the logic, even after I checked the result and found it correct. I have tried to follow the method for other situations, particularly where m1 = -0.5 and tried various values of m2 such as -1, -1.5, -2, -2.5 just to keep the sums easy for my poor old brain. It only seems to work for m2 = -1.5 and I'm still mystified as to how OP managed to hit on a rule that seems to work only in this particular situation. Did he know the answer and notice the convenient y=x/3 relation at the corner, then spot the rule?

BTW I'm also looking at his other post and am equally befuddled by his explanation of how he gets the right answer. Where the numbers in the √( ...) come from I just can't see. Clearer explanations are needed if we are to check the work.

Its true that i knew the answer, the rule may not be mathematically correct... it's just my way of thinking in trying to find a connection between the two acceleration values in this case 'gradients' by my definitive term 'the so called ' scale factor'. I am not ruling this out, its something that i may want to explore further as i study more on Mechanics...for the other post you are talking about, i would state that it follows all mathematical principles like indicated. Cheers.

 

[chwala]

What is the "desired line"? Why is it parallel to y=x/3? There are an infinite number of lines parallel to y=x/3. Why that one in particular?

I was interested on the parallel line that has gradient $\frac {-3}{2}$ and this line has to intersect the line $v=-0.5t+30$ and $v$=$\frac {1}{3}t$, where the points of intersection would give us the required co ordinates.

 

[Merlin3189]

I was interested on the parallel line that has gradient $\frac {-3}{2}$ and this line has to intersect the line $v=-0.5t+30$ and $v$=$\frac {1}{3}t$, where the points of intersection would give us the required co ordinates.

The question is, why does the line HAVE to intersect $v=-0.5t+30$ and $v$=$\frac {1}{3}t$ ?
You only know that after you have the answer.

If the two accelerations had been say -0.5 m/sec/sec and -2 m/sec/sec, where your "scale factor" is 4, would you draw the line $v$=$\frac {1}{4}t$, and expect to draw a line of gradient $\frac {-4}{2}$ through the intersection?
When I tried it, the required line was about v= 0.3 t , though not so conveniently exact.

 

[chwala]

The question is, why does the line HAVE to intersect $v=-0.5t+30$ and $v$=$\frac {1}{3}t$ ?
You only know that after you have the answer.

If the two accelerations had been say -0.5 m/sec/sec and -2 m/sec/sec, where your "scale factor" is 4, would you draw the line $v$=$\frac {1}{4}t$, and expect to draw a line of gradient $\frac {-4}{2}$ through the intersection?
When I tried it, the required line was about v= 0.3 t , though not so conveniently exact.

That is a "wild' thought that i came up with...i may need to explore further on that...of course you may disapprove my approach with a counter example...i will also try create different problems on this and try use my 'scale factor'. That's the beauty of Maths, we have to try think out of the box and that does not mean that i am correct.

 

[chwala]

The answer is correct, but I don't get the logic here:

Why do you plot y = x/3?
You don't use the fact that you are given the total stopping distance. You could make the change in acceleration at any point during the first stage, and the stopping distance would be different. Did you get the right answer by coincidence?
I plotted a v-t graph and worked out the distance (area under the curve) as a function of T, the time at which the acceleration is changed, and solved the quadratic equation in T.

Would you mind sharing your approach? ...am thinking,
Using, $v=u+at$ for the last part where the deceleration was increasing, we would have;
$0=-1.5t+30$
$1.5t=30$
$t=2$ then using, $s$=$ut$+$\frac {1}{2}$$at^2$, we shall have the distance in the last portion being given by,
$s$=$(30×2)$+$\frac {1}{2}$$(-1.5×4)=57$
$804-57=747$ Therefore, for the first part, i.e $v =0.5t+30$, we shall have the distance being given by
$747$=$\frac {-1}{4}$$t^2$ +$30t$. On solving this quadratic equation, we end up with
$t_1=35.26$ and $t_2=84.7$... is this a correct approach or i have missed out something?... the correct value is $t=36$.

 

[mjc123]

.of course you may disapprove my approach with a counter example..

I have already disproved it by pointing out that there is an infinite number of points where the two v-t curves might intersect. Only one of them gives the total stopping distance of 804 m. You have to use this information to get the right answer. I have no idea what you are thinking with your "scale factor". It does indeed seem to be a "wild thought".

 

[chwala]

I have already disproved it by pointing out that there is an infinite number of points where the two v-t curves might intersect. Only one of them gives the total stopping distance of 804 m. You have to use this information to get the right answer. I have no idea what you are thinking with your "scale factor". It does indeed seem to be a "wild thought".

Ok, let me share my thoughts on this...as i explore further. Remember i came up with the idea of 'scale factor' to connect the two gradients...we have two gradients here and the latter one i.e a=$-1.5$, forms my point of reference. I assumed this gradient to come from the origin, which is the $v=30$m/s, then having this line i was interested in finding the other parallel line that will intersect the other line with gradient, a=$-0.5$ and this was made possible by the line $v$=$\frac{1}{3}t$ that was found using my so called 'scale factor'.
Of course i am not implying that this is correct, i just need more time to explore further by looking at my own created examples i.e if you have not done so...

This is how it looks like;

I take cognizant of your comments though and i really appreciate. Thanks mjc

 

[mjc123]

I drew this v-t plot. The area under the curve (rectangle + 2 triangles) is the distance covered (804 m). Express this as a function of T and solve for T.

 

[chwala]

I drew this v-t plot. The area under the curve (rectangle + 2 triangles) is the distance covered (804 m). Express this as a function of T and solve for T.
View attachment 294417

nice...

$-2T^2+240T-6048=0$
$T=36$ or $T=84 (Unsuitable)$

 

[pbuk]

You don't need to use graphs and invent a 'scale factor' law to solve this.

Like most suvat problems the approach is to select the correct equation. Here you are given distance (s), initial velocity (u), final velocity (v) and acceleration (a), and the equation that relates them is $v^2 = u^2 + 2 a s$. The complication is that the deceleration is split into two parts: $-0.5 m/s$ for $s_1$ metres and $-1.5 m/s$ for $(804 - s_1)$ metres. Can you write down two equations in the form $v^2 = u^2 + 2 a s$ that describe the motion?

 

[chwala]

You don't need to use graphs and invent a 'scale factor' law to solve this.

Like most suvat problems the approach is to select the correct equation. Here you are given distance (s), initial velocity (u), final velocity (v) and acceleration (a), and the equation that relates them is $v^2 = u^2 + 2 a s$. The complication is that the deceleration is split into two parts: $-0.5 m/s$ for $s_1$ metres and $-1.5 m/s$ for $(804 - s_1)$ metres. Can you write down two equations in the form $v^2 = u^2 + 2 a s$ that describe the motion?

I tried that approach but didn't go anywhere...I will look at it ...

 

[chwala]

Ok, looks like finding it analytically creates some chaos...
using,
$v^2=u^2+2as$, we have
$(-1.5t+30)^2=30^2+(2×-0.5)s_1$.........1
$0 =(-1.5t+30)^2+(2×-1.5)s_1$......2

it follows that

$(-1.5t+30)^2=30^2+(2×-0.5)s_1$.........3
$- (-1.5t+30)^2 =+(2×-1.5)s_1$..........4

then,

$(-1.5t+30)^2=900-1s_1$.........5
$- (-1.5t+30)^2 =-3s_1$........6

taking (5) - (6), we shall have

$0 = 900-s_1-3s_1$
$900= 4s_1$→$s_1=225$

substituting $s_1=225$ into equation (1), yields

$2.25t^2-90t+225=0$
$t_1= 37.3$ and $t_2 2.679$... i would like to know why my steps are not leading to solution...of course you may have used the same formula with some variation...

 

[pbuk]

Ok, looks like finding it analytically creates some chaos...
using,
$v^2=u^2+2as$, we have
$(-1.5t+30)^2=30^2+(2×-0.5)s_1$.........1

There shouldn't be any t's in there, we are looking for an equation in the form $v^2=u^2+2as$. The first equation covering the period when acceleration is 0.5 m/s is $v_1^2 = 30 ^ 2 + 2 (-0.5) s_1$.

Now write an expression in the form $v^2=u^2+2as$ for the period when acceleration is 1.5 m/s. The only unknowns should be $v_1$ and $s_1$.

 

[chwala]

There shouldn't be any t's in there, we are looking for an equation in the form $v^2=u^2+2as$. The first equation covering the period when acceleration is 0.5 m/s is $v_1^2 = 30 ^ 2 + 2 (-0.5) s_1$.

Now write an expression in the form $v^2=u^2+2as$ for the period when acceleration is 1.5 m/s. The only unknowns should be $v_1^2$ and $s_1$.

ok, just correct me if for the first equation we have, $u=30$m/s then it follows that $v_1=-0.5t+30$ m/s...

 

[chwala]

Ok, going with your thinking the two equations are,
$v_1=900-s_1$
$0= v_1-3s_1$
which still gives $s_1=225$

 

[pbuk]

ok, just correct me if for the first equation we have, $u=30$m/s then it follows that $v_1=-0.5t+30$ m/s...

Well you could write $v_1=-0.5t_1+30$ but that wouldn't help you because you can't find another expression involving only $v_1$ and $t_1$.

Ok, going with your thinking the two equations are,
$v_1=900-s_1$

Shouldn't that be $v_1^2$?

$0= v_1-3s_1$

Again, $v_1^2$. And if the car travels $s_1$ metres while it is decelerating at 0.5 m/s/s and $804$ metres in total before comes to a stop, how far does it travel while it is decelerating at 1.5 m/s/s?

 

[chwala]

Well you could write $v_1=-0.5t_1+30$ but that wouldn't help you because you can't find another expression involving only $v_1$ and $t_1$.

Shouldn't that be $v_1^2$?

Again, $v_1^2$. And if the car travels $s_1$ metres while it is decelerating at 0.5 m/s/s and $804$ metres in total before comes to a stop, how far does it travel while it is decelerating at 1.5 m/s/s?

yes its $v_1^2$...I still don't not get it, I found $s_1=225$metres and if the car decelerates at $0.5$$m/s^2$ then it took time $t=8.03$ and $t=111.96$...which is not correct.

 

[chwala]

I Nailed it!Bingo!

Let the unknown co ordinate be denoted by $(t,v)$ i.e at the point of intersection of the two gradients and let the co-ordinate crossing the $x-axis$ be denoted by $(t_1,0)$
then, it follows that,
$\frac {v-30}{t-0}$=$\frac {-1}{2}$ and
$\frac {v-0}{t-t_1}$=$\frac {-3}{2}$

$→v=30-0.5t$
$→v=-1.5t+1.5t_1$

$30-0.5t=-1.5t+1.5t_1$
$1.5t_1=30+t$
→ $t_1$= $\frac {30+t}{1.5}$
Therefore

$804$= $\frac {1}{2}$$[\frac {30+t}{1.5}+t]$$v$+$\frac {1}{2}$×$t$$(30-v)$
$1608$=$[\frac {30+t+1.5t}{1.5}]$$v$+$t(30-v)$
$2412=(30+2.5t)v+1.5t(30-v)$
$2412=30v+2.5tv+45t-1.5tv$
$2412=30v+45t+tv$
$2412-45t=30v+tv$
$v(30+t)=2412-45t$
$v$=$[\frac {2412-45t}{30+t}]$ We know that
$[\frac {-1}{2}]$=$[\frac {v-30}{t-0}]$ therefore,
$[\frac {-1}{2}]$=$[\frac {2412-45t}{30+t}-30]$ ×$[\frac {1}{t}]$
$[\frac {-1}{2}]$=$[\frac {2412-45t-900-30t}{30+t}]$×$[\frac {1}{t}]$
$\frac {-1}{2}$=$\frac {1512-75t}{30t+t^2}$ it follows that,
$-30t-t^2=3024-150t$
$t^2-120t+3024=0$
giving us, $t_1=36$ and $t_2=84$

 

[pbuk]

yes its $v_1^2$...I still don't not get it, I found $s_1=225$metres and if the car decelerates at $0.5$$m/s^2$ then it took time $t=8.03$ and $t=111.96$...which is not correct.

That's because you have ignored the second part of my post:

And if the car travels $s_1$ metres while it is decelerating at 0.5 m/s/s and $804$ metres in total before comes to a stop, how far does it travel while it is decelerating at 1.5 m/s/s?

 

[chwala]

I managed to create my own problem on this and changed the values as indicated on my graph below; just to see whether the 'scale factor' may be an approach that can be adopted on such kind of problems.

note that i have my total distance as $1200m$, initial velocity as $40$ and the acceleration values as $-0.25$ and $-2$ respectively, We are trying to find the time at the highlighted point just like what we did on our previous problem.
Now using mjc's approach in post $13$, calculating this would give me

$\frac {1}{2}$$[\frac {51200-320T-160T+T^2}{32}]$+$\frac {160T-T^2}{4}$+$\frac {T^2}{8}$=$1200$

$51200-320T-160T+T^2)+16(160T-T^2)+4T^2=76800$

$-11T^2+2080T+51200=76800$

$-11T^2+2080T-25600=0$

$T_1=13.233$ and $T_2$=$175.85$,

Now on using the scale factor approach, reference post $1$,
i will intend to find the scale factor $m$, where

$-2m$=$\frac {-1}{4}$

$m$=$\frac {1}{8}$

Now we have three set of equations to plot;

1. $v=-0.25t+40$

2. $v=-2t+40$

3. $v$=$\frac {1}{8}$$t$

The point of intersection of equation $3$ and equation $1$, will give us the time that we are looking for. On plotting this we get;

Note that the value found is an approximate value with a difference of $0.1$ seconds from the exact value.

 

[mjc123]

Again, it can only be coincidence, as you haven't used the total distance, and you get a unique answer where there are infinite possible answers depending on the value of the distance. For instance, if the total distance was 1000 m, there would be a different value of T, but your method would give the same as before.

 

[chwala]

Again, it can only be coincidence, as you haven't used the total distance, and you get a unique answer where there are infinite possible answers depending on the value of the distance. For instance, if the total distance was 1000 m, there would be a different value of T, but your method would give the same as before.

True, I see your point...if $$s$$ would be a different value, then we may not have the same $$T$$ values. Thanks mjc...