Zekes
- 4
- 0
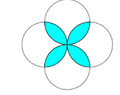
So, say you got 4 circles intersecting this way:
View attachment 9061
Now, I am looking for two things:
Now, in my search to finding the answer to this, I stumbled upon this Circle-Circle Intersection -- from Wolfram MathWorld. The only problem? I have no idea what this article is trying to say, and how it can help me. I did find the equation to get the area of the shaded region ( it's $$A=2(\pi-2)$$ ) which I can use in Part 2 but I still don't understand how the solution got to there, and how to do Part 1. Please help me in learning what is trying to be said here in simpler terms! Thanks!
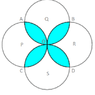
View attachment 9061
Now, I am looking for two things:
A proof that each part of the circle which is in an intersection is 1/4 the size of the whole circle's circumference
The exact area of the non-shaded region.
Now, in my search to finding the answer to this, I stumbled upon this Circle-Circle Intersection -- from Wolfram MathWorld. The only problem? I have no idea what this article is trying to say, and how it can help me. I did find the equation to get the area of the shaded region ( it's $$A=2(\pi-2)$$ ) which I can use in Part 2 but I still don't understand how the solution got to there, and how to do Part 1. Please help me in learning what is trying to be said here in simpler terms! Thanks!
Attachments
Last edited: