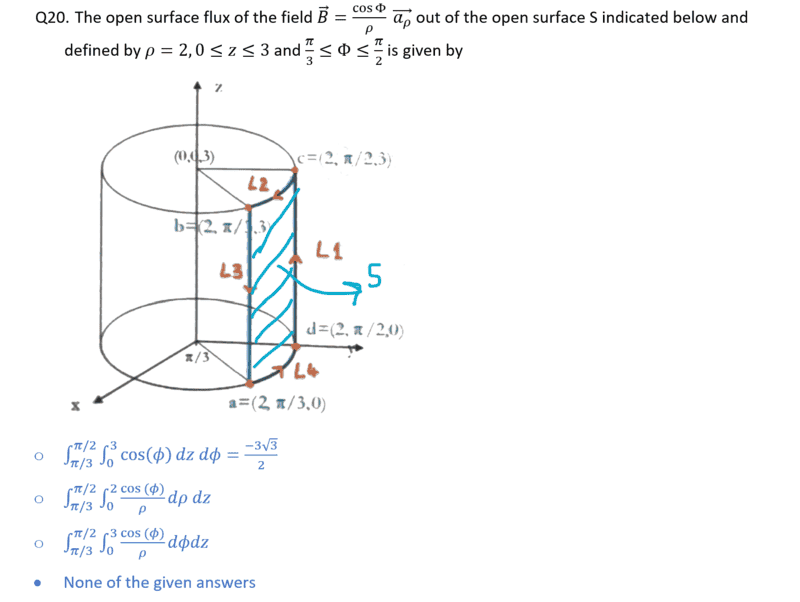
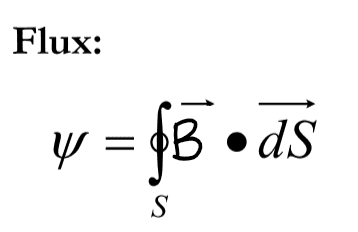SUMMARY
The discussion centers on the proper methodology for calculating the flux of a vector field. A participant critiques an initial attempt, highlighting the incorrect equating of vector and scalar quantities and the misuse of the multiplication symbol in vector analysis. The correct approach requires a clear motivation for using specific variables, such as ##\rho##, and emphasizes the importance of obtaining an exact result rather than an approximation. The conversation underscores the necessity of adhering to vector analysis conventions to achieve accurate results.
PREREQUISITES
- Understanding of vector fields and flux calculations
- Familiarity with vector analysis notation and operations
- Knowledge of scalar and vector quantities
- Proficiency in mathematical expressions involving variables like ##\rho##
NEXT STEPS
- Study the principles of vector calculus, focusing on flux integrals
- Learn about the divergence theorem and its applications in vector fields
- Explore the correct use of vector notation and operations in mathematical expressions
- Practice solving vector field problems with an emphasis on exact results
USEFUL FOR
Students and professionals in mathematics, physics, and engineering who are involved in vector analysis and flux calculations will benefit from this discussion.