- #1
RFeynman
- 7
- 0
- Homework Statement
- Calculate the field $$(\Phi_{SN})_{*} \frac{\partial}{\partial u}$$
- Relevant Equations
- $$(s,t) = (\Phi_{SN})(u,v) = \frac{1}{u^2 + v^2}(u,v)$$
$$\frac{\partial}{\partial u} = \frac{\partial s}{\partial u}\frac{\partial}{\partial s} + \frac{\partial t}{\partial u} \frac{\partial}{\partial t} $$
I identified $$(\Phi_{SN})_{*})$$ as $$J_{(\Phi_{SN})}$$ where J is the Jacobian matrix in order to $$(\Phi_{SN})$$, also noticing that $$\frac{\partial}{\partial u} = \frac{\partial s}{\partial u}\frac{\partial}{\partial s} + \frac{\partial t}{\partial u} \frac{\partial}{\partial t} $$, I wrote the first equation as:
(Its also worth pointing out that $$\frac{\partial}{\partial u} = [1,0]^T$$)
$$(\Phi_{SN})_{*} \frac{\partial}{\partial u} = J_{(\Phi_{SN})} [1,0]^T$$ and after some calculations I got some gibberish, I plotted it and got this:
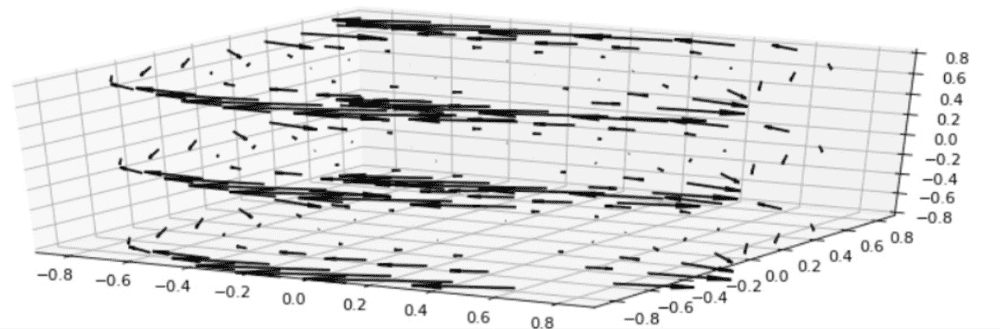
I think this is incorrect, in my idea the vector field should be like the contour of a circumference. Am I doing some wrong when calculating the vector field or my procedure is correct?
Thank you very much for helping!
(Its also worth pointing out that $$\frac{\partial}{\partial u} = [1,0]^T$$)
$$(\Phi_{SN})_{*} \frac{\partial}{\partial u} = J_{(\Phi_{SN})} [1,0]^T$$ and after some calculations I got some gibberish, I plotted it and got this:
I think this is incorrect, in my idea the vector field should be like the contour of a circumference. Am I doing some wrong when calculating the vector field or my procedure is correct?
Thank you very much for helping!