rstein66
- 6
- 0
Problem: In the circuit shown in the figure below, the capacitors C1 and C2 have
a capacitance of 45µF. C3 and C4 have a capacitance of 90µF. The two
terminals A and B on the left have a potential difference of 25V
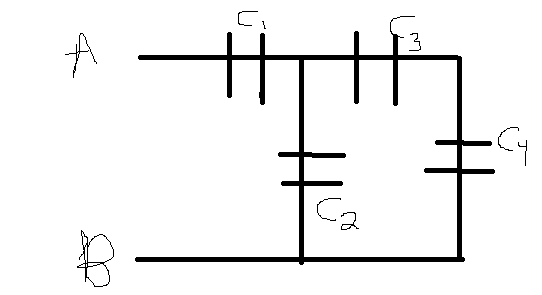
(Sorry - had to quickly draw it, could not save/find image)
(a) Find the magnitude of charge stored in the entire network.
(b) Find the magnitude of charges stored in each capacitor.
(c) Find the energy stored in each capacitor. Identify the capacitor with
the largest energy content.
(d) The C3 capacitor is now removed from the circuit, leaving a break
in the wire at its position. What is the voltage drop across the three
remaining capacitors?
(e) Describe how the maximal amount of energy can be stored using
these four capacitors. Draw the resulting circuit and state how much
energy is stored in your circuit using the same potential difference of
25V.
Equations/etc:
C=Q/V
Ceq series=(1/c1+1/c2...)^-1
Ceq parallel=c1+c2...
Series capacitors have equal charges and different voltages while parallel's have different charges and equal voltages.
U=(CV^2)/2 (Energy of capacitors)
Attempt:
a) Q1234=C1234(V)
Knowing that C1 and C3 are in series , C13=3e-5F
C2 and C4 in parallel, thus C24 = 1.34e-4F
C13 and C24 are in series thus C1234=2.45e-5F
Thus Q1234=C1234*V=2.45e-5F*25V=6.1e-4C
b)Since C1 and C3 are series, Q1=Q3=Q13=Q1234=C1234(V)=2.45e-5F*25V=6.1e-4C
I am not sure how to then solve Q2 and Q4 assuming I did Q1, Q3 correctly.
c) U=(CV^2)/2 , I realize that C for each is already given but am not sure what are the individual voltages.
d) I am unsure how to approach this
e) Since Ceq parallel is greater then the individual capacitance then it would make sense for it to be an all parallel circuit where the new Energy is equal to U=(CV^2)/2 where C=C1+C2+C3+C4.
Thanks.
a capacitance of 45µF. C3 and C4 have a capacitance of 90µF. The two
terminals A and B on the left have a potential difference of 25V
(Sorry - had to quickly draw it, could not save/find image)
(a) Find the magnitude of charge stored in the entire network.
(b) Find the magnitude of charges stored in each capacitor.
(c) Find the energy stored in each capacitor. Identify the capacitor with
the largest energy content.
(d) The C3 capacitor is now removed from the circuit, leaving a break
in the wire at its position. What is the voltage drop across the three
remaining capacitors?
(e) Describe how the maximal amount of energy can be stored using
these four capacitors. Draw the resulting circuit and state how much
energy is stored in your circuit using the same potential difference of
25V.
Equations/etc:
C=Q/V
Ceq series=(1/c1+1/c2...)^-1
Ceq parallel=c1+c2...
Series capacitors have equal charges and different voltages while parallel's have different charges and equal voltages.
U=(CV^2)/2 (Energy of capacitors)
Attempt:
a) Q1234=C1234(V)
Knowing that C1 and C3 are in series , C13=3e-5F
C2 and C4 in parallel, thus C24 = 1.34e-4F
C13 and C24 are in series thus C1234=2.45e-5F
Thus Q1234=C1234*V=2.45e-5F*25V=6.1e-4C
b)Since C1 and C3 are series, Q1=Q3=Q13=Q1234=C1234(V)=2.45e-5F*25V=6.1e-4C
I am not sure how to then solve Q2 and Q4 assuming I did Q1, Q3 correctly.
c) U=(CV^2)/2 , I realize that C for each is already given but am not sure what are the individual voltages.
d) I am unsure how to approach this
e) Since Ceq parallel is greater then the individual capacitance then it would make sense for it to be an all parallel circuit where the new Energy is equal to U=(CV^2)/2 where C=C1+C2+C3+C4.
Thanks.