Homework Help Overview
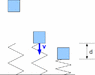
The problem involves a block dropped onto a spring characterized by a spring constant \( k \). The block has a speed \( v \) just before impact and compresses the spring by a distance \( d \) before coming to rest. The objective is to determine the mass of the block based on these parameters.
Discussion Character
- Exploratory, Conceptual clarification, Assumption checking
Approaches and Questions Raised
- Participants discuss energy conservation principles, questioning the initial conditions and the role of kinetic and potential energy in the system. There are various attempts to set up energy equations, with some participants suggesting different interpretations of initial velocity and height.
Discussion Status
The discussion is ongoing, with participants exploring different methods to relate the energies involved. Some have provided insights into the conservation of energy, while others are clarifying assumptions about initial conditions and the definitions of variables. There is no explicit consensus yet on the correct approach or final answer.
Contextual Notes
Participants note the lack of information regarding the initial height from which the block is dropped, which complicates the analysis. There are also discussions about the implications of setting the zero point for potential energy and how it affects the calculations.