mathlearn
- 331
- 0
Data
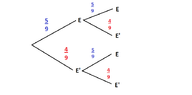
Below are the possible observations of a random experiment in a tree diagram.Each time it is observed whether the event E defined in part i occurs or not.
View attachment 5990Where do I need help
Find the probability that E' occurs at least once
Many Thanks :)
Below are the possible observations of a random experiment in a tree diagram.Each time it is observed whether the event E defined in part i occurs or not.
View attachment 5990Where do I need help
Find the probability that E' occurs at least once
Many Thanks :)
Attachments
Last edited: