MHB Find the ratios of the areas of the four regions

  • Thread starter Thread starter Bobbobstubob
  • Start date Start date
  • Tags Tags
    Areas Ratios
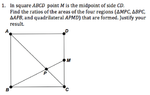
AI Thread Summary
The discussion focuses on finding the area ratios of four regions formed in square ABCD by point M, the midpoint of side CD. It highlights that triangles MPC and APB are similar, which is crucial for determining the area ratios. Participants suggest using properties of similar triangles to derive the necessary ratios. The conversation emphasizes the importance of justification in the calculations to ensure accuracy. Overall, the goal is to clearly establish the area ratios of ∆MPC, ∆BPC, ∆APB, and quadrilateral APMD.
Bobbobstubob
Messages
1
Reaction score
0
In square ABCD point M is the midpoint of side CD. Find the ratios of the areas of the four regions (∆MPC, ∆BPC, ∆APB, and quadrilateral APMD) that are formed. Justify your result.View attachment 8047
 

Attachments

  • IMG_1624_01.png
    IMG_1624_01.png
    12.7 KB · Views: 107
Mathematics news on Phys.org
Re: Having a difficult time figuring out how to solve this

Hello, and welcome to MHB! (Wave)

I think my first step would be to explain how $\triangle MPC$ and $\triangle APB$ are similar, from which we can determine the ratio of their areas...
 

Thread 'Non-orthogonal bases'

Suppose ,instead of the usual x,y coordinate system with an I basis vector along the x -axis and a corresponding j basis vector along the y-axis we instead have a different pair of basis vectors ,call them e and f along their respective axes. I have seen that this is an important subject in maths My question is what physical applications does such a model apply to? I am asking here because I have devoted quite a lot of time in the past to understanding convectors and the dual...
View full post »

Thread 'Fermat's Last Theorem'

Fermat's Last Theorem has long been one of the most famous mathematical problems, and is now one of the most famous theorems. It simply states that the equation $$ a^n+b^n=c^n $$ has no solutions with positive integers if ##n>2.## It was named after Pierre de Fermat (1607-1665). The problem itself stems from the book Arithmetica by Diophantus of Alexandria. It gained popularity because Fermat noted in his copy "Cubum autem in duos cubos, aut quadratoquadratum in duos quadratoquadratos, et...
View full post »
Thread 'Imaginary Pythagorus'

Thread 'Imaginary Pythagorus'

I posted this in the Lame Math thread, but it's got me thinking. Is there any validity to this? Or is it really just a mathematical trick? Naively, I see that i2 + plus 12 does equal zero2. But does this have a meaning? I know one can treat the imaginary number line as just another axis like the reals, but does that mean this does represent a triangle in the complex plane with a hypotenuse of length zero? Ibix offered a rendering of the diagram using what I assume is matrix* notation...
View full post »

Similar threads

MHB [ASK] Find the ratio of the area of triangle BCH and triangle EHD
Replies
4
Views
2K
MHB Ratio of areas of squares - Challenging problem
Replies
1
Views
2K
MHB How to Find the Area of Quadrilateral ABCD with Given Side Lengths and Angles?
Replies
2
Views
2K
MHB How can I find the area of a triangle with a given angle and two sides?
Replies
2
Views
1K
MHB Area of the bounded regions between a straight line and a polynomial
Replies
1
Views
986
MHB Find the area of the quadrilateral PQRS
Replies
4
Views
2K
MHB Area of Triangle Shaded Region
Replies
5
Views
2K
MHB Find the ratio of lines in a circle
Replies
3
Views
2K
MHB Find Measure of ∠BAD in ABCD Rhombus
Replies
3
Views
2K
MHB Max Area of Simple Quadrilateral w/ Sides $a$ & $b$: Justification
Replies
4
Views
2K

Hot Threads

Recent Insights

Back
Top