Find the refractive index for the lens and find the image distance

[Karl Karlsson]

Homework Statement

A thin lens has an upper radius of curvature 𝑅1 and a lower radius of curvature 𝑅2. When the lens is completely surrounded by air, it has a focal distance 𝑓. The lens is then placed in the interface between air and water inside a vessel (see figure). Calculate the refractive index for the glass and the distance below the water surface on which the image of a distant object will end up?

Relevant Equations

A thin lens has an upper radius of curvature 𝑅1 and a lower radius of curvature 𝑅2. When the lens is completely surrounded by air, it has a focal distance 𝑓. The lens is then placed in the interface between air and water inside a vessel (see figure). Calculate the refractive index for the glass and the distance below the water surface on which the image of a distant object will end up?

A thin lens has an upper radius of curvature 𝑅1 and a lower radius of curvature 𝑅2. When the lens is completely surrounded by air, it has a focal distance 𝑓. The lens is then placed in the interface between air and water inside a vessel (see figure). Calculate the refractive index for the glass and the distance below the water surface on which the image of a distant object will end up?

The refractive index for water is given to nc = 1.33 and for air na = 1.00

My attempt:

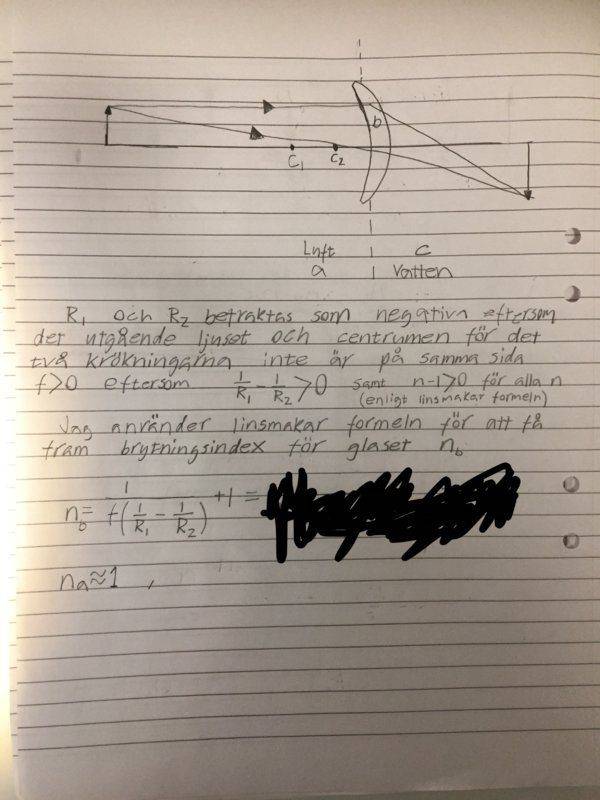
Is my solution correct? I have nowhere to check the answer and I have not done any similar problem before. Have I missed something?

 

[TSny]

Your work looks good to me. But, they might want you to express the final answer in terms of the givens: $f$, $R_1$, $R_2$, $n_{air}$, and $n_{water}$.

 

[Karl Karlsson]

Your work looks good to me. But, they might want you to express the final answer in terms of the givens: $f$, $R_1$, $R_2$, $n_{air}$, and $n_{water}$.

I assumed the refractive index for water was given because I could not solve the problem without it. Can the problem be solved if one only knows the refractive index for air?

 

[TSny]

I assumed the refractive index for water was given because I could not solve the problem without it. Can the problem be solved if one only knows the refractive index for air?

You can assume $n_{water}$ to be known. But since no numerical values are given in the statement of the problem, I don't think you will need to use a particular value for $n_{water}$.

I think they want you to express your answers in terms of the symbol $n_{water}$ as well as the given symbols $R_1$, $R_2$, and $f$. Here, $f$ is the focal length with air on both sides of the lens.

For the first question, you found the index of refraction of the glass in terms of these symbols and it looks right.

Your answer to the second question also looks correct to me. But I was wondering if you are expected to express your answer in terms of only the "given" symbols $R_1$, $R_2$, and $f$ (as well as $n_{water}$). It could be that the way you expressed the answer is completely adequate. It depends on your instructor.