SUMMARY
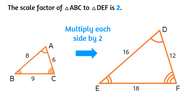
Triangles ABC and DEF are similar, with triangle ABC having a perimeter of 16 cm and triangle DEF having sides measuring 6 cm, 8 cm, and 10 cm, resulting in a perimeter of 24 cm. The scale factor of triangle ABC to triangle DEF is definitively 2/3, as established by the ratio of their perimeters (16:24). The dilation scale factor, which is a transformation from triangle ABC to triangle DEF, is 3/2. Therefore, the correct answer to the question regarding the scale factor is not D (3/2) but rather 2/3.
PREREQUISITES
- Understanding of similar triangles
- Knowledge of perimeter calculations
- Familiarity with scale factors and ratios
- Basic concepts of dilation in geometry
NEXT STEPS
- Study the properties of similar triangles in geometry
- Learn how to calculate perimeters of various geometric shapes
- Research the concept of dilation and its applications in transformations
- Explore practical examples of scale factors in real-world scenarios
USEFUL FOR
Students studying geometry, educators teaching similar triangles, and anyone interested in understanding geometric transformations and scale factors.