Find the slope of the secant to the curve f(x)=-3logx+2 between these points:

[Vela1]

The question was too long to post in the title so I just wrote down the first part. I hope this is alright. Here is the question that I am doing right now:

This is the graphical representation (thanks to Desmos Graphing Calculator):

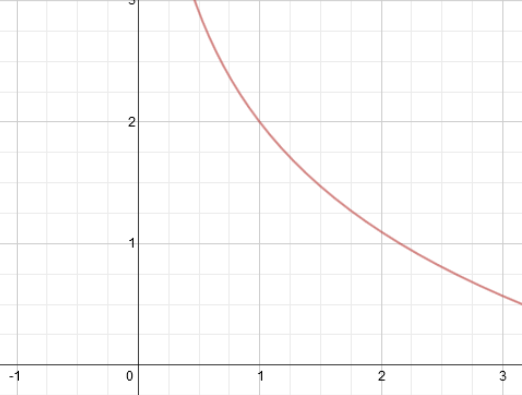
So I have substituted the points in the equation to get their respective y-values.
For example:

f(1.1) = -3log(1.1)+2
f(1.1) =~ 1.87

I've done the questions myself using this method to find the slope of the secant line, and I wanted confirmation that I was doing it right.

----------------------------------

I've written it on paper and unfortunately I don't have a scanner so I will just type out (i) and (ii) to show my rationale.

4.a)

i] m = (Y2-Y1) / (X2-X1)
= (1.097-2) / (2-1)
= -0.903 / 1
m = -0.903

ii] m = (Y2-Y1) / (X2-X1)
= (1.472-2) / (1.5-1)
= -0.528 / 0.5
m = -1.056

------------------------------------------------

I just wanted to know if I was doing it correctly, and if not how can I answer this question? Thanks in advance.

 

[Ackbach]

Your example shows you're using $\log(x)=\log_{10}(x)$. If so, it appears your first one is correct; I didn't bother to check the second, as it's analogous. Looks fine to me!

 

[Vela1]

OK, thank you. I just have one more question:

This is the second part to question #4. I wanted to do it myself before I confirmed my answer here.

Here are my steps:

I found the derivative of the initial equation: f(x) = -3log(x)+2

The derivative was: f(x) = (-3) / (ln[10] x (x))

So I substituted 1 for x, and the answer I got was -1.303. I rounded it to 3 decimal places. Is this the correct method, or is there another way?

Thanks in advance.

 

[MarkFL]

Yes, you are doing fine. I think what I would do is recognize all four questions are the same except for one parameter, $\Delta x$. So I would derive a formula into which I could then just plug into. In other words, work the problem once instead of four times.

The slope is given by:

\(\displaystyle m=\frac{\Delta f}{\Delta x}=\frac{f\left(x+\Delta x \right)-f(x)}{\Delta x}\)

Now, using the given definition of $f(x)$, we may write:

\(\displaystyle m=\frac{\left(-3\log\left(x+\Delta x \right)+2 \right)-\left(-3\log\left(x \right)+2 \right)}{\Delta x}=\frac{3\log\left(\frac{x}{x+\Delta x} \right)}{\Delta x}\)

With $x=1$, there results:

\(\displaystyle m=\frac{3\log\left(\frac{1}{1+\Delta x} \right)}{\Delta x}\)

a) \(\displaystyle \Delta x=1\)

\(\displaystyle m=\frac{3\log\left(\frac{1}{1+1} \right)}{1}=-3\log(2)\approx-0.903\)

b) \(\displaystyle \Delta x=\frac{1}{2}\)

\(\displaystyle m=\frac{3\log\left(\frac{1}{1+\frac{1}{2}} \right)}{\frac{1}{2}}=6\log\left(\frac{2}{3} \right)\approx-1.057\)

Now just plug-n-chug for the remaining two. :D

The formula we derived will be very useful in answering part b). Let $\Delta x$ get smaller and smaller until two successive results agree to 3 decimal places. Or, as you did, you can use calculus, but I suspect you are not expected to be able to differentiate.

 

[CellCoree]

I can confirm that your method for finding the slope of the secant line is correct. You have correctly substituted the given points into the equation and used the formula for slope to calculate the values. Your answers for both (i) and (ii) are correct. However, it is always a good idea to double check your work and ensure that your answers make sense in the context of the graph. In this case, the negative slopes make sense as the curve is decreasing from left to right. Keep up the good work!