- #1
Davidllerenav
- 424
- 14
- Homework Statement
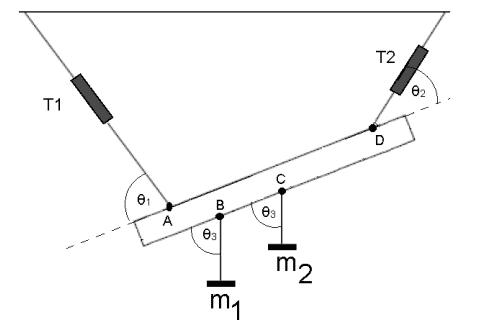
- A rule of weight ##w## is supported by two strings and inclined with respect to the horizontal as shown the figure. From the points ##B## and ##C## of the rule hang two masses ##m_1## and ##m_2##. Considering that the system is in mechanical equilibrium, calculate the tensions in the strings ##T_1## and ##T_2##. Consider that point ##C## it's in the middle of the rule (Important: To simplify the system solution, consider only the condition ##Pτ = 0## at points ##A## and ##D##.)
- Relevant Equations
- ##\sum \vec F=0##
##\sum \tau = 0##
I tried to do the free body diagram of the problem, but I{m confused because the rule is inclined. Should I just use the given angles to calculate the forces on x and y? Also, how should I calculate the torques? Since I don't know the dimensions of the rule. Can you help me? I think that once I understand how to set up the diagrams I woudl be able to understand. Thr figure of the problem is shown below.