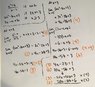FritoTaco
- 132
- 23
Homework Statement
Find the values of a and b that make f continuous everywhere.
See attachment for the function.
I'm suppose to find a and b.
Homework Equations
The Attempt at a Solution
See the second attachment
The problem I have is, when I get to the last step, I'm trying to cancel out b so I can get just a. When I do that by manipulating the equation (multiplying (3) and (6) the orange writing you see on the board) it ends up canceling out a (so both a and b). Did I go wrong somewhere?