Find the volume of the hexagonal-shaped plastic box

  • Context: MHB 
  • Thread starter Thread starter angubk6
  • Start date Start date
  • Tags Tags
    Box Plastic Volume
Click For Summary

Discussion Overview

The discussion revolves around finding the volume of a hexagonal-shaped plastic box used to pack triangular chocolate bars. Participants explore the relationship between the dimensions of the chocolate bars and the box, including the need to calculate the volume of the bars to determine the box's volume.

Discussion Character

  • Homework-related
  • Exploratory
  • Technical explanation

Main Points Raised

  • One participant suggests that the volume of the hexagonal box can be determined by first calculating the volume of each triangular chocolate bar and multiplying it by 24.
  • Another participant questions whether the problem is asking for the height of the chocolate bar or the side length, indicating a need for clarification.
  • A mathematical expression for the height of the chocolate bar is provided, $h = \dfrac{3}{2}\tan(50^\circ)$, which is relevant for calculating the volume of the bars.
  • Concerns are raised about the lack of information regarding the measurements of the hexagonal box, suggesting that more details are needed to solve for the side length of the chocolate bar, $x$.
  • Repeated requests for the complete problem statement and previous attempts to solve it are made to facilitate assistance.

Areas of Agreement / Disagreement

Participants express uncertainty about the necessary information to solve the problem, indicating that there is no consensus on how to proceed without additional details.

Contextual Notes

The discussion highlights limitations in the provided information, particularly regarding the dimensions of the hexagonal box and the chocolate bars, which are essential for solving the problem.

angubk6
Messages
2
Reaction score
0
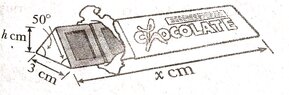
A chocolate company produces triangular chocolate bars. The length of the chocolate bar is x cm, and its cross section is an isosceles triangle. The length of the base side of the cross section is 3 cm, the height is h cm, and the two base angles are 50 degrees.
View attachment 9689

Moreover, the company uses a hexagonal-shaped plastic box to pack 24 chocolate bars together as shown in the figure below.
View attachment 9690

What is the volume of the hexagonal-shaped plastic box?

*I would like to apologize if I keep on editing the content of my problem. Originally, the question asked was to find the volume of the hexagonal shaped plastic box. In my opinion, I can only solved this if I will be able to find the volume of each triangular chocolate bars then multiply it by 24 (please correct me if my view was invalid). However, I am really having a hard time in solving for x.
 

Attachments

  • CamScanner 04-18-2020 16.06.12_1.jpg
    CamScanner 04-18-2020 16.06.12_1.jpg
    164.9 KB · Views: 133
  • CamScanner 04-18-2020 21.51.28_1.jpg
    CamScanner 04-18-2020 21.51.28_1.jpg
    185.9 KB · Views: 99
Last edited:
Mathematics news on Phys.org
Is it asking you for the height of the chocolate bar, or the side length?

Have you drawn a diagram?
 
$h = \dfrac{3}{2}\tan(50^\circ)$

You’ll need the bar’s volume to determine the length of the bar, $x$.
 
*I would like to apologize if I keep on editing the content of my problem. Originally, the question asked was to find the volume of the hexagonal shaped plastic box. In my opinion, I can only solved this if I will be able to find the volume of each triangular chocolate bars then multiply it by 24 (please correct me if my view was invalid). However, I am really having a hard time in solving for x.

What measurement information was given about the hexagonal box? As it sits, there is not enough information to determine $x$.
 
angubk6 said:
*I would like to apologize if I keep on editing the content of my problem. Originally, the question asked was to find the volume of the hexagonal shaped plastic box. In my opinion, I can only solved this if I will be able to find the volume of each triangular chocolate bars then multiply it by 24 (please correct me if my view was invalid). However, I am really having a hard time in solving for x.

Post the entire problem to start with, with everything you have tried, and then we can actually help you!
 

Similar threads

MHB [ASK] Find the volume of Pyramid in a Cube
  • · Replies 6 ·
Replies
6
Views
3K
MHB Ilovethepopper's question at Yahoo Answers concerning the width of a hexagon
  • · Replies 1 ·
Replies
1
Views
2K
Undergrad Curiosity about infinity in geometry(Not homework just curious)
  • · Replies 2 ·
Replies
2
Views
2K
MHB Finding a particular angle withion Johnson Solid J2
  • · Replies 2 ·
Replies
2
Views
2K
High School Volume of a Cube: Definition & Explanation
  • · Replies 7 ·
Replies
7
Views
5K
MHB Riemanns Sum Problem: Find the exact volume
  • · Replies 1 ·
Replies
1
Views
2K
MHB Volume of a Tetrahedron: General Slicing Method
  • · Replies 1 ·
Replies
1
Views
5K
MHB Can You Find the Angle in This Isosceles Triangle Problem?
  • · Replies 1 ·
Replies
1
Views
1K
Determing the center of gravity of a shaded section
  • · Replies 14 ·
Replies
14
Views
2K
MHB Find the Volume of Mt. Vesuvius After 79AD in Terms of pi
  • · Replies 3 ·
Replies
3
Views
2K