Discussion Overview
The discussion focuses on finding two values of $\theta$ within the range $0^{\circ} < \theta < 360^{\circ}$ that satisfy specific trigonometric equations: $\sin\theta=\frac{1}{2}$, $\cos\theta=-\frac{\sqrt{3}}{2}$, and $\csc\theta=-\sqrt{2}$. The participants explore methods for solving these equations without the use of a calculator, emphasizing the importance of understanding special angles and their properties.
Discussion Character
- Homework-related
- Mathematical reasoning
- Conceptual clarification
- Exploratory
Main Points Raised
- Some participants note that $\theta = 30^{\circ}$ is a solution for part a) and seek to find the other solution.
- One participant suggests identifying the quadrants where $\sin(\theta) > 0$ to narrow down potential solutions.
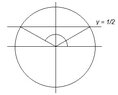
- Another participant proposes visualizing the problem using the unit circle and the line $y=\frac{1}{2}$ to find the angles where the sine function meets this value.
- There is a discussion about using the identity $\sin(\pi - \theta) = \sin(\theta)$ to find the second angle associated with the first solution.
- Participants explore the relationship between angles in different quadrants and how to derive them from known values.
Areas of Agreement / Disagreement
Participants generally agree on the method of finding solutions through the unit circle and the properties of trigonometric functions, but the discussion remains unresolved regarding the exact values for all parts of the problem, particularly for parts b) and c).
Contextual Notes
Participants rely on knowledge of special angles and trigonometric identities, but there are no explicit resolutions for parts b) and c), and the discussion does not cover all necessary assumptions or steps for those parts.