member 731016
- Homework Statement
- Please see below
- Relevant Equations
- Please see below
For this problem,
Find ##A^{-1}## given,
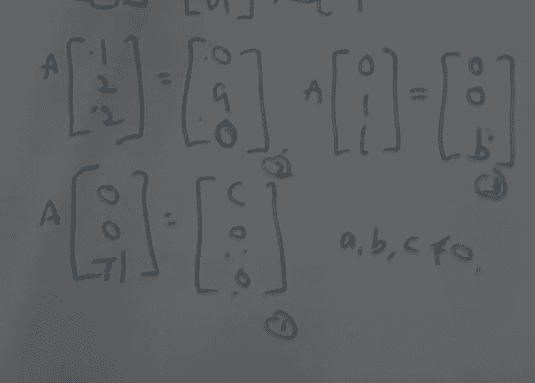
The solution is,
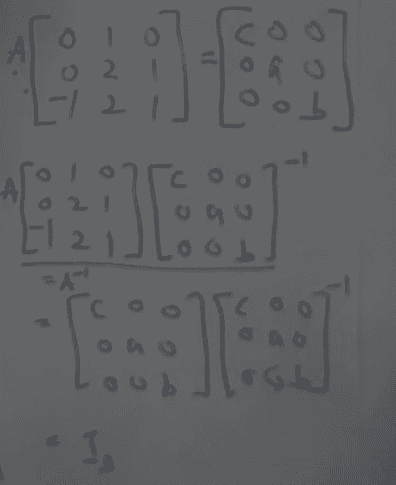
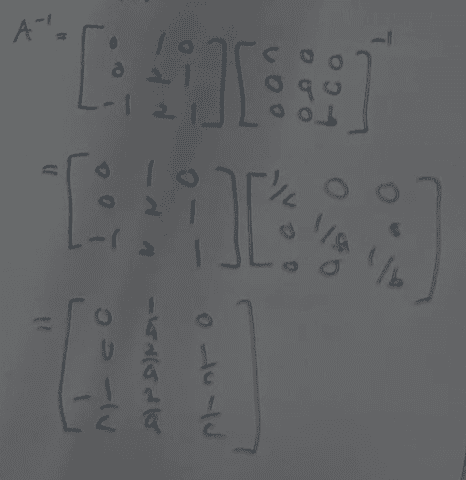
However, in the first image, why are we allowed to put together the submatrices in random order? In general does someone please know why we are allowed to decompose matrices like this?
Many thanks!
Find ##A^{-1}## given,
The solution is,
However, in the first image, why are we allowed to put together the submatrices in random order? In general does someone please know why we are allowed to decompose matrices like this?
Many thanks!
Last edited by a moderator: