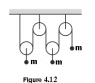
- #1
Aireaz
- 1
- 0
Homework Statement
All the masses of the black dots are the same, the pulleys and ropes are massless.
Calculate the acceleration of the right most object (the one that is just on the single hanging rope)
Homework Equations
Fnet= ∑F : ma=T-mg
d= v1t + 1/2at^2
The Attempt at a Solution
The left pulley and the middle pulley can be thought of as one system, therefore ma1 = 4T-2mg
The right pulley is simply ma2=mg - T
If the right rope was pulled down a distance of d then the two ropes on the middle and left rope will go up d/2 making it d= 4 * 1/4d. This means looking at the acceleration formula, d = 1/2a2t^2 (v1=0) and 1/4d = 1/2a1t^2, I found that a2=4a1 (as 1/4d=1/2a1 isolate for d which is d=2a1 which substituted in d=1/2a2 gets 2a1=1/2a2 giving 4a1=a2)
now it can be substituted into the fnet equation. if a1=-a2/4 (since one pulley accelerates in one direction and the other in the opposite direction). ma1=4T-2mg becomes m(-a2/4) = 4T-mg and will yield (-ma2+8mg)/16 = T
T can be substituted in the other fnet equation leading to ma2 = mg - (-ma2+8mg)/16 which calculated yields 16ma2 = 16mg - 8mg + ma2 and finally leads into 15a2=8g.
the answer should be a2=8g/15 however something is wrong as this is not an answer that is correct. Can someone help me see what is incorrect?