Finding an open-cicuit voltage, why is resistor in series ignored?

[justin___]

Homework Statement

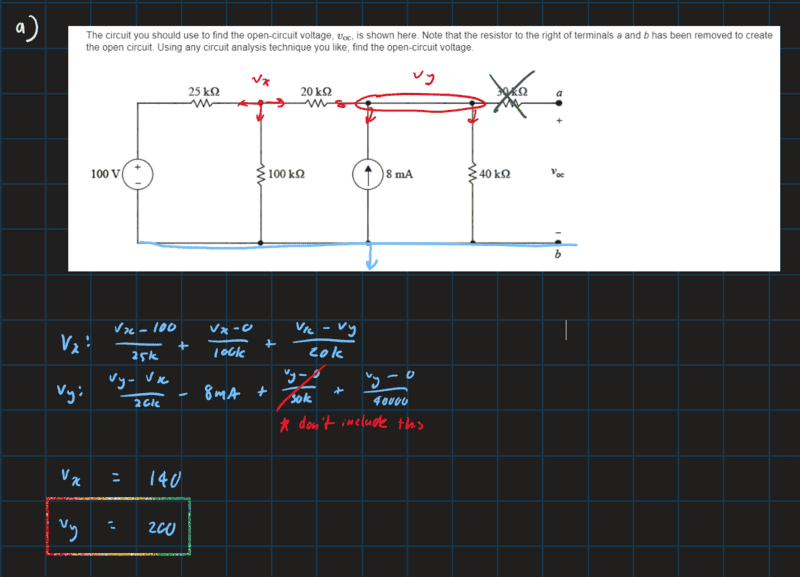
The circuit you should use to find the open-circuit voltage, voc, is shown here. Note that the resistor to the right of terminals a and b has been removed to create the open circuit. Using any circuit analysis technique you like, find the open-circuit voltage.

Relevant Equations

KCL

I found how to get the solution to this question (the answer is 200V), but I don't understand why we ignore the 30kOhm resistor when using analysing the circuit. Because it is in series with the open voltage, wouldn't there be some voltage drop across the resistor that would affect the open-circuit voltage?

Thanks

 

[Tom.G]

Hint:
Can you write the equation for the voltage drop across a resistor given its value and the current thru it?

Upon inspection of that equation, the light bulb above your head will likely come on.

Cheers,
Tom

 

[justin___]

Hint:
Can you write the equation for the voltage drop across a resistor given its value and the current thru it?

Upon inspection of that equation, the light bulb above your head will likely come on.

Cheers,
Tom

Thanks for the hint. So because the 30kOhm resistor is in series with an open circuit, no current flows through it, therefore there is no voltage drop and we can ignore it from the equation?