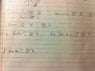Finding E and V involving 2 planes.

[xxbigelxx]

Homework Statement

Two large planes have uniform charge density. Plane 1 is located at z₁=-4 cm and has charge density σ₁=-10μC/cm2. Plane 2 is located at z₂=+6 cm and has charge density σ₂=+20μC/cm2.
a. Determine E(x,y,z) in the 3 regions.
b. Determine V for all points. Choose V=0 at plane 2.
c. Briefly describe the equipotentials, draw and label at least 3 of them.

Homework Equations

The Attempt at a Solution

I know that Gauss Law has to be used. I am just a bit confused on the concept that the charge distributions aren't equal. This is throwing me off a little bit. Do I find the Q-enclosed for both individually, then add them?

 

[kuruman]

Yes, you calculate the E-field from each plate separately (as if the other one were not there) and then add the fields vectorially in each of the three regions. That's what "superposition" means.

 

[xxbigelxx]

I got E=10uC/2epsilon-naught for between the plates, E=-10uC/2epsilon-naught for the upper plane, and E=20uC/2epsilon-naught for the bottom plate. Does this seem correct? I am still a tad confused.

 

[xxbigelxx]

I tried to think of this in other manners, but wasn't successful. Any thoughts are welcome. Thanks again.

 

[kuruman]

I got E=10uC/2epsilon-naught for between the plates, E=-10uC/2epsilon-naught for the upper plane, and E=20uC/2epsilon-naught for the bottom plate. Does this seem correct? I am still a tad confused.

This does not seem correct. Start with E = σ/(2ε₀) and list separately the values of the field E₁ in each of the three regions and of E₂ in each of the three regions (6 numbers altogether). It would help if you drew a picture and don't forget that field lines go towards the negatively charged plate on both sides and away from the positively charged plate on both sides.

 

[xxbigelxx]

Hmm this is what I attempted to do. I have attached my work to this post to see if you can give me some pointers as to where I made a mistake. Thanks.

Edit: I don't know why the picture is rotated. It's not like that when I upload it. Sorry.

 

[kuruman]

I do not understand the arrows that you have drawn in the figure. Draw two arrows, no more no less, side by side in each region to represent the fields contributed by each plate. Then we'll have something to talk about.

 

[Mindscrape]

The two plates should have have piecewise functions of E, in other words, E for left of the plate, and E for right of the plate. Try doing that to get the electric fields right, and then your superposition should follow. Your magnitudes are right though.

 

[xxbigelxx]

Ok this is my updated drawing. For some reason the attachment was failing so I had to upload it elsewhere...

http://i53.tinypic.com/11bnkm9.jpg

 

[xxbigelxx]

Mindscrape: what do you mean to the right and to the left of the plates? shouldn't it be to the top and bottom of them? Thanks.

 

[kuruman]

The top plate is positively charged and the bottom plate is negatively charged. You have the arrows mixed up. Also in the in-between regions you have more than two arrows and have not labeled any of them, so it is not clear which arrow is contributed by which plate.

 

[xxbigelxx]

Oh I had read the problem wrong. Ok I fixed the directions of my arrows. For the in-between regions I only have two arrows, the other lines are my coordinate axes. (the 'x' I drew is the origin.) I hope this makes it easier to follow.

Should I draw four arrows in the middle, even though they all point in the same direction? Two for each plate's contribution?

 

[kuruman]

Should I draw four arrows in the middle, even though they all point in the same direction? Two for each plate's contribution?

There are only two plates, so in each region there should be only two arrows, one from each plate.

 

[xxbigelxx]

Ohh I think/hope I got it now. The right column of vectors are the contributions of the bottom plate. The left column are for the top plate.

 

[Mindscrape]

Yeah, there you go. Yes, I did mean top and bottom earlier, I was looking at your sideways drawing. :)

 

[xxbigelxx]

Haha ok good. So now, I draw 3 different Gaussian surfaces?

 

[kuruman]

Ohh I think/hope I got it now. The right column of vectors are the contributions of the bottom plate. The left column are for the top plate.

OK, so now put in the numbers and add the two arrows in each region. Don't forget that up is positive and down is negative.

 

[xxbigelxx]

Ok I think I got part a. Any comments?

 

[kuruman]

No comments. Looks OK.

 

[xxbigelxx]

Ok great. So for part b, do I take my values for E, and integrate over dz?

 

[Mindscrape]

Yep, give it a try.

 

[xxbigelxx]

Ok these are my integrals. I am a bit confused on the bounds. Did I set them up correctly?

 

[kuruman]

Your upper limit should not be infinity because you are looking for the potential as a function of z. Also, the left side of the equation should be
V(at the upper limit of the integral) - V(at the lower limit of the integral)

V is taken to be zero only at the top plate, not anywhere else.

 

[xxbigelxx]

Ok I think I fixed both of my errors. Hopefully my equation for the bottom plate is correct. The directions got a bit confusing.

 

[kuruman]

You actually need to evaluate the integrals to get functions that depend on z, V(z), in each region. I don't understand why some of your limits are y. What does y represent? And what is V(y)? Does your potential change when you keep the distance z from each plate and move sideways thus changing y only?

 

[xxbigelxx]

Right I didn't want to evaluate them until I got the bounds correct. And those aren't y's (sorry for my handwriting) they are supposed to be 4's since -4 is the location of Plate 1.

 

[kuruman]

Then you're fine except that the upper limits for all integrals must be "z" with no negative sign because you are finding V(z) where z is an algebraic quantity that can be positive or negative. Also, be sure you find V(-4) relative to the zero that is given.

 

[xxbigelxx]

Ok for the top section, I got the V(z)-V(6)= (-5/epsilon-naught)z.
For the bottom I got V(z)-V(-4)= (-5/epsilonnaught)[z-4]
For between I got V(-4)-V(6)=60/epsilonnaught

 

[noface]

Why wouldn't the top section be V(6)-V(z), if for the other two regions the potential at the lower z-value was subtracted from that at the higher z-value [for V(z)-V(-4), z is "below" -4, and for V(-4)-V(6), -4 is "below" 6]?

 

[xxbigelxx]

Hmm I am not sure. Maybe it's just dependent on the magnitude of the distance. Hopefully Kuruman can help us whenever they return.