Discussion Overview
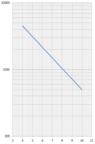
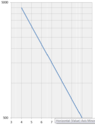
The discussion revolves around finding an equation that represents a line on a logarithmic graph, specifically focusing on a line that descends towards zero. Participants explore the nature of the graph, the appropriateness of different mathematical models, and the potential issues with the graph's scale.
Discussion Character
- Exploratory
- Debate/contested
- Mathematical reasoning
Main Points Raised
- One participant is attempting to derive an equation of the form y=a*b^x but finds discrepancies between their calculations and the graph.
- Another participant suggests that a linear model may suffice since the line appears straight, questioning the need for a more complex approach.
- Concerns are raised about the accuracy of the y-axis scale, with some participants speculating that the logarithmic scale might be incorrectly represented.
- One participant calculates the slope of the line segment between two points on the graph and finds it matches a derived formula, but expresses confusion over discrepancies in commission values at certain prices.
- There is a suggestion that the graph's numbers may be misaligned, proposing that adjusting the scale could resolve the confusion regarding the equation's accuracy.
Areas of Agreement / Disagreement
Participants express differing views on whether a linear model is appropriate versus a logarithmic model. There is also uncertainty regarding the accuracy of the graph's scale, with no consensus on the correct representation of the data.
Contextual Notes
Participants note limitations in understanding the logarithmic scale being used and the potential misalignment of values on the graph, which may affect the interpretation of the equation.