member 731016
- Homework Statement
- I am trying to understand whether part (c) of the problem below is wrong. I have also provided my working and the solutions.
- Relevant Equations
- Sequence notation ##\{a_n\}##
For this problem,

My working is
##\{\frac{a_{n + 2}}{a_{n+1}}\} = \{1 + \frac{a_n}{a_{n +1}}\}## using part (b)
Then
##\lim_{n \to \infty} b_n = \lim_{n \to \infty} (1 + \frac{a_n}{a_{n +1}})## which should equal ##L##.
However, does someone please know why it does this cause the sequence to converge to ##L##. The solution does not explain anything (just simply states the definition):
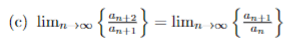
Any help greatly appreciated.
Many thanks!
My working is
##\{\frac{a_{n + 2}}{a_{n+1}}\} = \{1 + \frac{a_n}{a_{n +1}}\}## using part (b)
Then
##\lim_{n \to \infty} b_n = \lim_{n \to \infty} (1 + \frac{a_n}{a_{n +1}})## which should equal ##L##.
However, does someone please know why it does this cause the sequence to converge to ##L##. The solution does not explain anything (just simply states the definition):
Any help greatly appreciated.
Many thanks!