Finding linear acceleration of a spool and cable

[haven]

Homework Statement

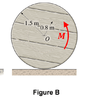
A constant counter-clockwise moment of M = 110 N-m is also applied to the spool. The spool and the cable are initially at rest. The spool has a mass of 550 kg, an outer radius of 1.5 m, and a radius of gyration of 1.3 m. Assume 2 SF for all givens.
Refer now to Figure B where the spool is allowed to roll on the ground, the tension T has been removed. If the spool rolls without slipping and has the same applied moment M as described above, what is the linear acceleration of the spool? Take right to be positive.
(include units with answer)

Relevant Equations

torque = I*a
a= r*angular acceleration + angular velocity^2*r
I=M*Ro^2

My angular acceleration is wrong but all I had done was torque which was 110 NM / I = 930 kg-m^2 and calculated 0.118 rad/s^2. But because this is wrong I am stuck and I have no idea how to find angular velocity to plug into the equation to find linear acceleration.

 

[TSny]

There is a reference to a cable, but it is not described in the problem statement. Can we assume that the cable plays no part in the question?

If the spool rolls without slipping, then the moment $M$ is not the only moment acting about the disk's center spool's central axis.

 

[kuruman]

Perhaps it might be easier to consider this. A moment τ = 110 N⋅m is equivalent to a force $F = \frac{110}{1.5}$ N applied at the rim of the wheel. Then you can write two separate Newton's laws for linear and angular acceleration and solve for the linear acceleration. Don't forget the force of static friction since the wheel is assumed to roll without slipping. Yes, you don't know the coefficient of static friction, but you don't need it either.

 

[haruspex]

Homework Statement:: A constant counter-clockwise moment of M = 110 N-m is also applied to the spool.

"also"? If this is the exact wording, it is clearly not the start of the question. Please post the whole text.

 

[Lnewqban]

Could this be the removed tension they refer to?
Note the coincident radii, as well as the unwrapping cable at 7 o’clock in both pictures.

 

[haven]

Perhaps it might be easier to consider this. A moment τ = 110 N⋅m is equivalent to a force $F = \frac{110}{1.5}$ N applied at the rim of the wheel. Then you can write two separate Newton's laws for linear and angular acceleration and solve for the linear acceleration. Don't forget the force of static friction since the wheel is assumed to roll without slipping. Yes, you don't know the coefficient of static friction, but you don't need it either.

but how do we solve for acceleration when we don't know the friction force either?

 

[haruspex]

but how do we solve for acceleration when we don't know the friction force either?

What you know is that it does not slip. This gives you a simple relationship between the linear acceleration and the rotational acceleration.

There are two ways you can use this.
You can take moments about the spool's centre, giving an equation involving the frictional force and the angular acceleration, then combine that with the horizontal F=ma equation.
Alternatively, take moments about the point on the ground contacted by the spool. With this method you have to understand that the linear acceleration of the spool contributes to the angular acceleration about that point. But it has the advantage of not involving the frictional force, so you don't need the F=ma equation.