- #1
LT72884
- 323
- 48
Ok, i have a question. First, i am an engineering student and have done all math requirements up to linear alg. HOWEVER, my geometry is terrible, oh so terrible and i need some spoon feeding right now because i am stuck on a problem.
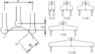
Ok, i saw a really cool tool the other day called a radius dial gauge. it measures the radius of an arc so if you are reverse engineering parts, you can find the radius of curvature if needs be.
here is a pic of it: the two end calipers do not move, they have a constant chord length of C. But different tools will have wider calipers to find bigger radii.
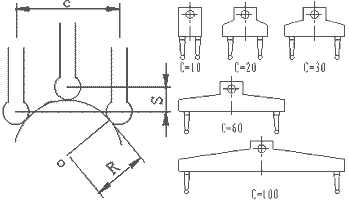
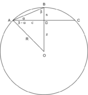
i am wanting to understand the math behind it. How do we find R based off of the constant chord length(C), the distance of the chord to the tangent surface of the circle? or S, the center point of the caliper
thank you so much for this help:)
Ok, i saw a really cool tool the other day called a radius dial gauge. it measures the radius of an arc so if you are reverse engineering parts, you can find the radius of curvature if needs be.
here is a pic of it: the two end calipers do not move, they have a constant chord length of C. But different tools will have wider calipers to find bigger radii.
i am wanting to understand the math behind it. How do we find R based off of the constant chord length(C), the distance of the chord to the tangent surface of the circle? or S, the center point of the caliper
thank you so much for this help:)