Finding specific weight of unknown fluid in a manometer

[Bolter]

Homework Statement

See below

Relevant Equations

N/A

Hey everyone!
Here is the problem I have been tackling but did not end up with the correct answer

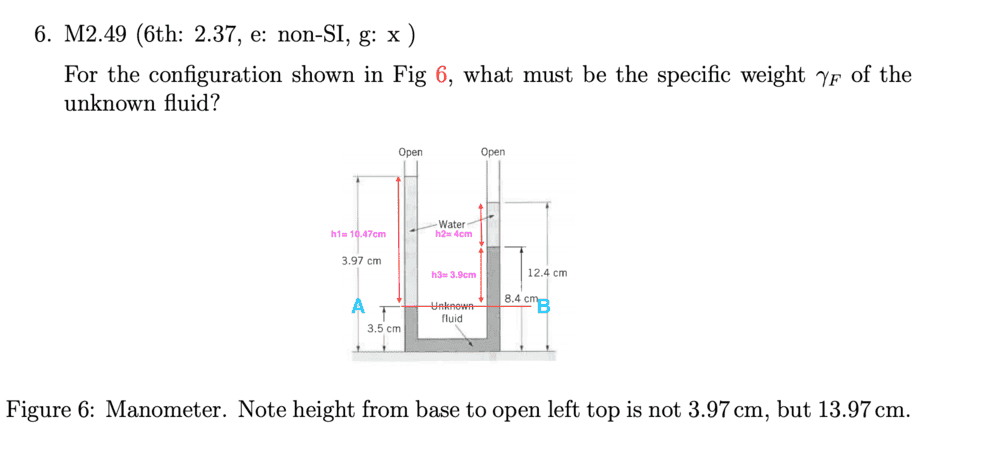
The extra red arrows I have labelled in myself and called these distances h1,h2 and h3. I assumed the pressure to be the same at levels A & B, hence i have established expressions for both of these and got the following

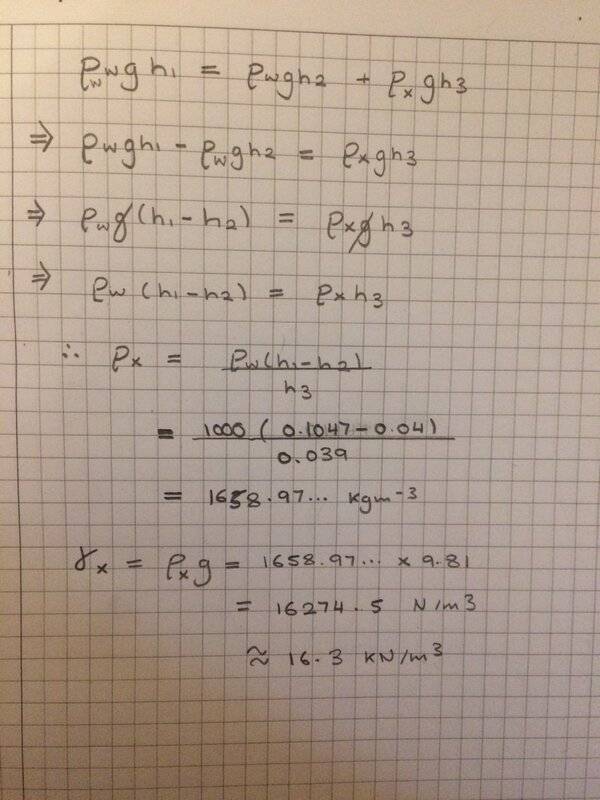
However this is not right and the right answer is actually 13.0 kN/m3. What did I do wrong exactly?

Thanks

 

[Bolter]

Nevermind I think I got the right answer now by doing something slightly different. I repositioned A & B to to be at the bottom of the manometer on both sides like this

I redid the method I used before in my first post. I got specific weight to come out as 12.95320... kN/m3 which is approx 13.0 kN/m3 to 3 sig figs

 

[kuruman]

Nevermind I think I got the right answer now by doing something slightly different. I repositioned A & B to to be at the bottom of the manometer on both sides like this

View attachment 270242
I redid the method I used before in my first post. I got specific weight to come out as 12.95320... kN/m3 which is approx 13.0 kN/m3 to 3 sig figs

Probably round off errors. My calculation according to the method in the original post gave, to 3 sig. figs., 1.32×10³ kg/m³. Note the correct units of density; the factor of $g$ cancels out.

 

[Bolter]

Probably round off errors. My calculation according to the method in the original post gave, to 3 sig. figs., 1.32×10³ kg/m³. Note the correct units of density; the factor of $g$ cancels out.

Its not asking for density, its asking for specific weight I believe which has units kN/m3

 

[kuruman]

You are absolutely correct.