Finding the Angle Between Two Forces

[Astrum]

Homework Statement

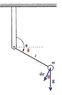
Question is in the attachment

Homework Equations

The Attempt at a Solution

I understand the concept and ideas, but the geometry evades me.

In polar coordinates, we have two components, $\hat{r},\hat{\theta}$

I know that you just integrate the dot product of $\vec{F}$ and $d\vec{r}$ with the boundaries of position, but how did we find the angle between the two vectors?!

 

[Simon Bridge]

Question is in the attachment

... the question in the attachment is:
"What is the velocity of m when the rod is at angle $\phi$?"
... which is answered in the rest of the attachment.

The geometry is circular. They drew you a diagram.
Probably what you need to do is redraw the diagram, bigger, for different values of $\phi$ - carefully draw in the vectors, resolve components, and watch how they change.

 

[Astrum]

... the question in the attachment is:
"What is the velocity of m when the rod is at angle $\phi$?"
... which is answered in the rest of the attachment.

The geometry is circular. They drew you a diagram.
Probably what you need to do is redraw the diagram, bigger, for different values of $\phi$ - carefully draw in the vectors, resolve components, and watch how they change.

I should have been clearer. I know the concept behind the problem, I know how they solved, just not where they go the [tex]cos(\varphi-\frac{\pi}{2}[itex]

That perplexes me. The dot product equals the magnitude of each vector multiplied by each other, times the cos of the angle between them.

I don't know how they determined the angle.

 

[TSny]

how did we find the angle between the two vectors?!

Can you show that the two angles marked θ in the picture are equal? [EDIT: The dotted line is horizontal]

 

[Simon Bridge]

I should have been clearer. I know the concept behind the problem, I know how they solved, just not where they go the $$cos(\varphi-\frac{\pi}{2} )$$

That perplexes me. The dot product equals the magnitude of each vector multiplied by each other, times the cos of the angle between them.

I don't know how they determined the angle.

... that is why I suggested you draw out the bigger diagrams. The exercise of resolving components gets you focussed on how the angles are related to each other. TSny has done one for you.

 

[Astrum]

I didn't even realize that those angles were equal...

I have not a clue how to prove they're equal.

 

[TSny]

Construct another horizontal auxiliary line through the mass m. Also think about how the vector dr is oriented relative to the rod.