Finding the differential equation of motion

[dbeckam]

Summary:: Differential equation of motion, parabola

Hi. I've tried resolve this problem but I have two doubts. The first is about the differential equation of motion because I can't simplify it to the form y" + a*y' + b*y = F(t). I'm not sure if what I got is right. My second doubt is that I cannot solve part b. Thank you in advance for your help.

In part a I got this: r"(R^2 + r^2) + (r'^2)r + g*r*R = 0.

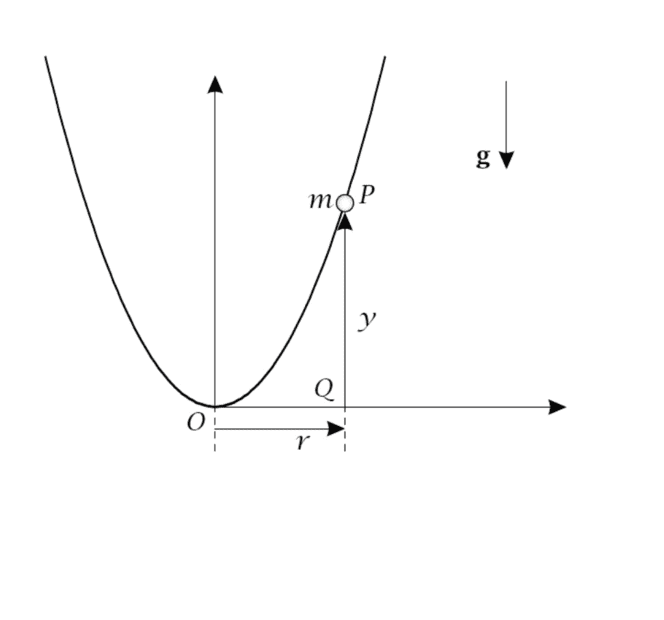
Problem:
A particle of mass m slides without friction along a fixed track in the form of a parabola. The equation of the parabola is y = (r^2)/(2R). R is a constant, r is the distance between O and Q, y is the vertical distance. Initial conditions: r(t=0) = r_0 and r'(t=0) = 0.

a) Find the differential equation of motion in terms of the variable r.
b) Find an expression for (r')^2 in function of r.

 

[ergospherical]

I agree with your equation of motion. The easiest way to find $\dot{r}$ is by considering the energy, which you should write as a function of $r$ and $\dot{r}$. The energy is conserved and equal to its initial value, $E(r,\dot{r}) = E_0$, which you can find from the initial conditions.

 

[Orodruin]

I can't simplify it to the form y" + a*y' + b*y = F(t)

Why do you think it should be possible to simplify it to this form? This form is in essence a driven harmonic oscillator with a friction term.

 

[dbeckam]

Why do you think it should be possible to simplify it to this form? This form is in essence a driven harmonic oscillator with a friction term.

Yes, I understand. Thanks!

 

[dbeckam]

I agree with your equation of motion. The easiest way to find $\dot{r}$ is by considering the energy, which you should write as a function of $r$ and $\dot{r}$. The energy is conserved and equal to its initial value, $E(r,\dot{r}) = E_0$, which you can find from the initial conditions.

I already resolved it. Thank you very much.