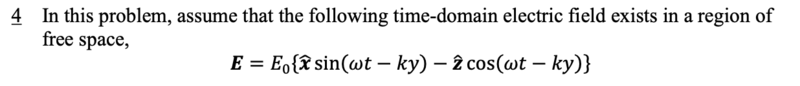SUMMARY
The discussion focuses on calculating the magnetic field (B) from the electric field (E) using Faraday's law in differential form, specifically the equation $$\nabla\times\mathbf{E}=-\frac{d\mathbf{B}}{dt}$$. Participants emphasize the importance of calculating the curl of E and integrating over time to derive B. Additionally, a correction is noted regarding the missing factor of $$\frac{1}{c}$$ in the expression for the magnetic field intensity (H). Understanding the relationship between the electric field, magnetic field, and wave propagation direction is crucial for solving the problem.
PREREQUISITES
- Understanding of Faraday's law of electromagnetic induction
- Knowledge of vector calculus, specifically curl and time integration
- Familiarity with electromagnetic wave propagation in free space
- Basic concepts of electric field (E) and magnetic field (B) relationships
NEXT STEPS
- Study the application of Faraday's law in electromagnetic theory
- Learn about vector calculus operations, particularly curl and divergence
- Explore the relationship between electric and magnetic fields in plane waves
- Investigate the implications of the speed of light (c) in electromagnetic equations
USEFUL FOR
Students and professionals in physics, electrical engineering, and anyone studying electromagnetic theory who seeks to deepen their understanding of the relationship between electric and magnetic fields in wave propagation.