Electron in a time variable magnetic field

[mahblah]

TL;DR Summary: Find acceleration of electron in dB/dt >0

Hello. Here is a problem that i'm not so sure about:

Inside a solenoid there is a time-dipendent magnetic field B, so we have dB/dt = b (constant).
We want to know the acceleration of an electron:
a) placed in the center of the solenoid
b) displaced of r=2cm from the center

The book report that:
case a)

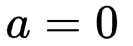
case b)

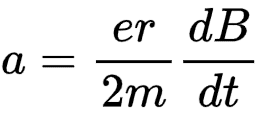
why should be different the result if the electron is placed in the center or in the displaced position? I can always imagine a "virtual circuit". Also, i think the electron "can't know where is placed".
Where am i wrong?
I've tried to solve the exercise by

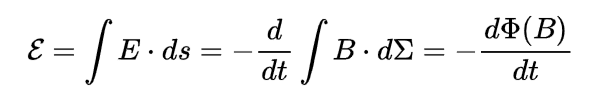
and i know i can get the result in this way:

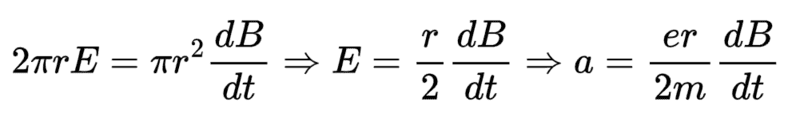
But this requires that "circle" is draw around the center.i could also draw this kind of circle (in orange) and so get a result for the electron in the center.

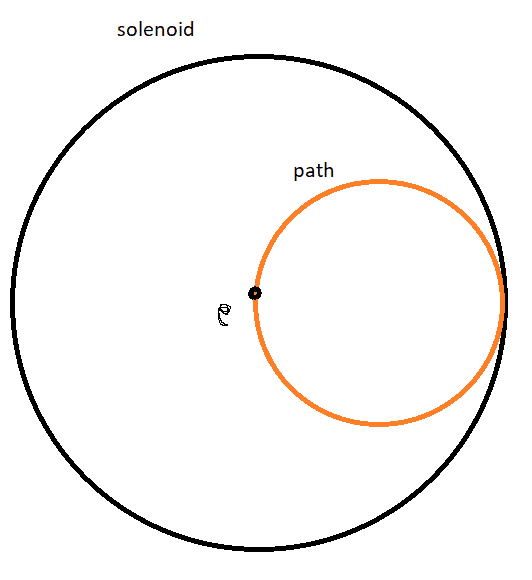
I have tried to find some answer looking for different path inside the solenoid (See below) but i'm not so convinced anyway.

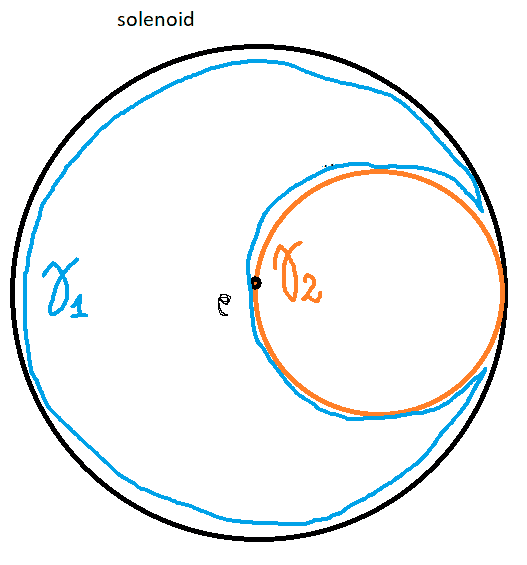Thanks anyone
sorry for the not-so-good post.

 

[Haborix]

You've recited that the electric fields depends on the distance from the center. What does that mean for the force on the electron due to the electric field? I don't know what virtual circuits have to do with anything, nor do I understand the comment about the electron not knowing where it is, especially in light of a spatially varying electric field. You can compute the electric field along your shifted loop but it will be more complicated since your choice of coordinates don't match the symmetry of the electric field about the center of the solenoid.

 

[TSny]

You'll need to think about the pattern of electric field lines inside the solenoid.

Note that going from $\oint \vec E \cdot \vec {ds}$ to $2 \pi r E$ requires the following:
(1) $\vec E$ is in the direction of $\vec {ds}$ at each point of the circular path of integration
(2) $|\vec E|$ is constant along the path.

So if you want to use $\oint \vec E \cdot \vec {ds} =2 \pi r E$, you will need to choose a circular path for which the above two conditions are satisfied.

 

[mahblah]

Thanks you both!
I think i've somewhat understand what you mean.

I have a side question, but probably is meaningless:
what can we say about the acceleration of an electron if all space is filled with dB/dt = b > 0 ?

 

[TSny]

I have a side question, but probably is meaningless:
what can we say about the acceleration of an electron if all space is filled with dB/dt = b > 0 ?

It's a good question. If all space is filled with dB/dt = b, then there isn't a unique solution for the electric field. To get a unique solution, you would need to add some extra information such as a boundary condition or symmetry condition.

The solenoid has rotational symmetry about the axis of the solenoid.

 

[mahblah]

Thanks again!