- #1
davidwinth
- 101
- 8
- Homework Statement
- Find the required force and angle for equilibrium
- Relevant Equations
- Included Sum of Forces equals zero
Hello,
I solved this problem two ways and got the same value for the magnitude but different values for the angle. I am wondering which is correct. I showed my work, so I hope someone can tell me if one method is just invalid.
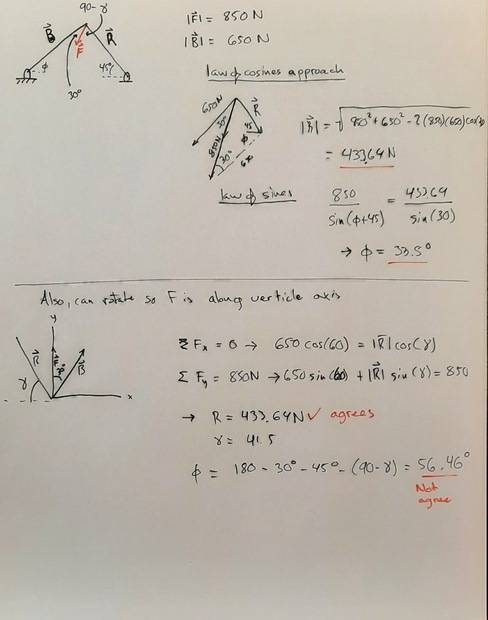
I solved this problem two ways and got the same value for the magnitude but different values for the angle. I am wondering which is correct. I showed my work, so I hope someone can tell me if one method is just invalid.
Last edited by a moderator: