Finding the Particle's Path: Graphing a Cartesian Equation

[Fatima Hasan]

Homework Statement

Identify the particle's path by finding a Cartesian equation for it . Graph the Cartesian equation . indicate the portion of the graph traced by the particle .
$x=2sinh t$ , $y=2cosh t$ , $-\infty < t < \infty$

Homework Equations

$cosh^2 t - sinh^2 t = 1$

The Attempt at a Solution

$sinh t = \frac{x}{2}$
Square both sides :
$sinh^2 t = \frac{x^2}{4}$ (1)
$cosh t = \frac{y}{2}$
Square both sides :
$cosh^2 t = \frac{y^2}{4}$ (2)
(2) - (1) :
$cosh^2 t - sinh^2 t = 1$
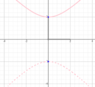
$\frac{y^2}{4} - \frac{x^2}{4} = 1$
put x= 0 → y=±2

Is my answer correct ?

 

[George Jones]

Is my answer correct ?

What do you know about the possible values of $\cosh t$ for $-\infty < t < \infty$?

 

[Fatima Hasan]

What do you know about the possible values of $\cosh t$ for $-\infty < t < \infty$?

The Cartesian equation forms a parbola opening up . Right ?

 

[George Jones]

I just noticed something else.
$$\frac{x^2}{4} - \frac{y^2}{4} =1$$
is not correct, but I think this is a "typo".

 

[Mark44]

The Cartesian equation forms a parbola opening up . Right ?

No. The graph you show is not a parabola.

 

[Mark44]

Identify the particle's path by finding a Cartesian equation for it .
Graph the Cartesian equation . indicate the portion of the graph traced by the particle .
$x=2sinh t$ , $y=2cosh2$ , $-\infty < t < \infty$

Should the second equation be $y = 2\cosh(t)$?

 

[Fatima Hasan]

Should the second equation be $y = 2\cosh(t)$?

yeah

 

[Mark44]

I agree with @George Jones's comment in post #4.

(2) - (1) :
$cosh^2 t - sinh^2 t = 1$
$\frac{x^2}{4} - \frac{y^2}{4} = 1$

Take a closer look at the work I've quoted above.

 

[Fatima Hasan]

$\frac{y^2}{4} - \frac{x^2}{4}$ forms a hyperbola and to graph it , we should go 2 units up from center point .
$cosh ( t)$ for $-\infty < t < \infty$ is always positive .

 

[Fatima Hasan]

I agree with @George Jones's comment in post #4.
Take a closer look at the work I've quoted above.

$\frac{y^2}{4} - \frac{x^2}{4} = 1$

 

[Mark44]

$\frac{y^2}{4} - \frac{x^2}{4} = 1$

Yes, that looks better.

 

[George Jones]

$\frac{y^2}{4} - \frac{x^2}{4} = 1$ forms a hyperbola

Yes, a big hint is given by the names of the functions in the original equations.

 

[Fatima Hasan]

Yes, that looks better.

Is it correct ?

 

[Mark44]

View attachment 231720
Is it correct ?

No.
The equation $\frac{y^2}{4} - \frac{x^2}{4} = 1$ is NOT a parabola. The graph you showed appears to be the graph of $y = x^2 + 2$, which is completely unrelated to your equation.

 

[Fatima Hasan]

The equation $\frac{y^2}{4} - \frac{x^2}{4} = 1$ is NOT a parabola.

 

[Mark44]

View attachment 231721

Bingo!
(Meaning, yes, that's it.)

 

[Fatima Hasan]

Bingo!
(Meaning, yes, that's it.)

Thanks for your help.