Finding the Radius (word problem)

[LCKurtz]

But yes that is the answer in the back of my trig book... How did you get that?
And I have a TI-89 calc..

I used Maple. With a program like that, there is little work to do. Here's the steps you type to solve it with Maple. I simplified it slightly for clarity:

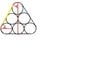
> equation1 := r*cos(alpha)+1 = r;
> equation2 := r*cos(beta)+2 = r;
> equation3 := r*(alpha+beta) = 6;

> fsolve({equation1,equation2,equation3}, {r, alpha, beta});

{r = 2.768080732, alpha = 0.8779382494, beta = 1.289628589}

> alphadegrees := evalf(180*alpha/Pi); 50.30215635

> betadegrees := evalf(180*beta/Pi); 73.89027526

Takes all the pain and suffering out of it, eh?

 

[Miike012]

I have another problem...

Six Identical pipes, each with radius of 1 foot are ties tightly together with a metal band... Find the length of the metal band...

I posted a picture...

My strategy is dividing the figure in half
Then finding the measure of the two arcs in red ( which should be equal)
Then finding the measure of the yellow line..
Once I find that... I can multiply it by three...
I am just not sure of how to do it...

 

[tiny-tim]

erm … page 3 ? …

for a new problem, best to start a new thread

 

[Miike012]

okay