Finding the shear centre of a non-homogeneous cross section cross

[Dell]

for the following cross section

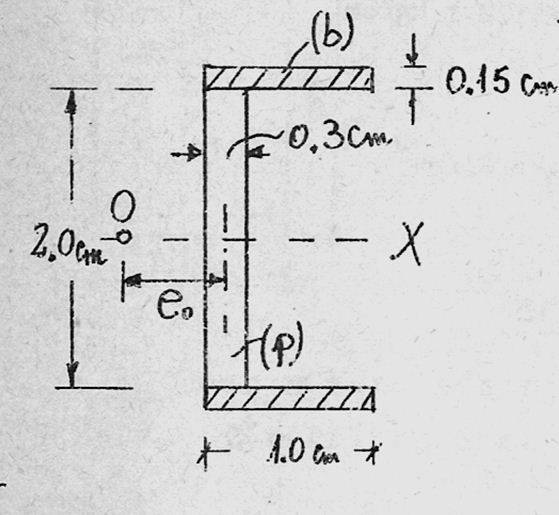
the ratio E^b/E^p=30

find the shear centre of the cross section
-------------------------------------------
first of all i need to find the equivalent cross section, which will be the same except that the horizontal parts will be of length n*L=30*1=30cm

since this cross section has an axis of symmetry, i know that the shear centre passes through that axis, now all i need to find is the distance "e_o"

i know that i can move the force to the shear centre and the cross section must feel the same moment, i calculated the moment about a point that passes through the Vertical portion so that only the sums of the horizontal shearing stresses have an effect on the moment,

i know that Q1y is the 1st area moment of each of the horizantal portions,

Q1y=(0.15*s)*1.075 =0.16125*s

I=10.6cm^4

shearing stress=\int\int(V*Q/I/b)da*2.15 where 2.15 is the distance between the horizontal forces

V*e=\int\int(V*Q/I/b)da*2.15

e=2.15/(I*0.15)*\intdt\intQds

e=[2.15/(I*0.15)]*0.15*\int(0.16125*s)ds -->from 0 to 30



[2.15/(10.6*0.15)]*0.15*0.16125*30²/2=14.7cm

the correct answer is somehow meant to be 0.408cm, can anyone see where i have gone wrong??

 

[pongo38]

your line: "shearing stress=LaTeX Code: \\int LaTeX Code: \\int (V*Q/I/b)da*2.15 where 2.15 is the distance between the horizontal forces"

comment: I'm not sure what all those integral signs are doing. I thought shearing stress was just V*Q/I/b. (That is, the result of integration). OK, so you multiply by area to get force, and then by 2.15 to obtain moment. So should your "shearing stress" read as "moment"?

 

[Dell]

o yes, that's correct, meant to be moment, but it still won't change the answer,

im beginning to think that the way i expanded the cross section was incorrect, i just made the 2 horizontals 30 times longer ( to the right) maybe i was meant to expand them to both sides, 14.5 to each side,

doing this would still not give me a correct answer, but much closer,
by doing this i get 0.49cm

is it possible that the answer i was given in the textbook (0.408) is incorrect,
could someone please check this for me