Transverse shear stress calculation in non-slender built up members

[greg_rack]

Homework Statement

Plates are made up of Aluminum(given max shear strength), nails are of given maximum shear force. Dimensions and load intensity are given. What will fail first, among the two plates and the nails?
DIAGRAM SHOWN BELOW

Relevant Equations

Shear formula

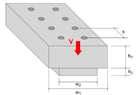
Hi guys, this is an exercise I have been tasked to solve for an assignment. First of explaining you what I have done to solve it using the shear equation, in order to find the maximum shear stress and the shear flow in the juncture, one big question:
how is it legal to utilize the shear formula in this case? One big limitation of it is given by the "aspect ratio" of the cross section; since to derive it the assumption of uniform shear distribution along the width has to be made, actual transverse stresses for flat cross sections(for this specific case, w1/h1 is approx. 4, whilst the threshold should be approx. 0.5) deviate significantly from the values predicted by the equation, since stress is not uniform along the width.
Thus, does the problem I've been given with even make sense? I'm quite confused

 

[Lnewqban]

The description of nails is confusing.
In real applications, those should be bolts that clamp both pieces of aluminum in such a way that friction helps them to keeps both pieces from sliding respect to each other in case of bending loads.

 

[greg_rack]

The description of nails is confusing.
In real applications, those should be bolts that clamp both pieces of aluminum in such a way that friction helps them to keeps both pieces from sliding respect to each other in case of bending loads.

True. But nails apart(e.g. let's say the same cross section was welded or extruded), would the shear formula apply? For the aspect ratio argument I reported above

 

[Lnewqban]

The shear formula applies to the cross-sections of the bolts or rivets.
The problem is to calculate the shear value caused by bending of the built-up beam at the intersection plane between both plates.
That value depends on the location of that plane respect to the neutral axis of the cross-section and the shear load distribution.

Please, see example problems here:
https://mathalino.com/reviewer/mech.../spacing-of-rivets-or-bolts-in-built-up-beams

 

[greg_rack]

The shear formula applies to the cross-sections of the bolts or rivets.

And why? isn't the transverse shear stress not uniformly distributed anymore, beeing the member(s) slender?

 

[Lnewqban]

And why? isn't the transverse shear stress not uniformly distributed anymore, beeing the member(s) slender?

Sorry, I don’t see why.
The rivets or bolts are only resisting the cutting effect of the “scissor” formed by both plates, which are trying to tightly slide respect to each other.
The bolts are keeping zero gap between the plates and the edges of the holes are the ones in charge of the cutting, regardless of the slenderness of each plate.

 

[greg_rack]

Sorry, I don’t see why.
The rivets or bolts are only resisting the cutting effect of the “scissor” formed by both plates, which are trying to tightly slide respect to each other.
The bolts are keeping zero gap between the plates and the edges of the holes are the ones in charge of the cutting, regardless of the slenderness of each plate.

View attachment 298141

Hey, sorry for responding just now.
What I meant is that, along the width of the cross section the shear stress will take up on different values... it's not going to be constant as maths in this case tells us. Always with respect to the distribution along the width, trans. shear stress value will be maximum at the edges and minimum at the center point; I think what answers my question is that with the shear formula we're just calculating the average shear stress along the width of the section. For an aspect ratio of the cross section of 2, the offset of this average stress to the actual maximum endured by the member is as high as of 40%, whilst for more slender members it can be very close to both the maxima and minima!