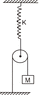Finding the time period of this System

[Hydrous Caperilla]

Homework Statement

To find the time period of this simple harmonic motion

Homework Equations

F= -kx

The Attempt at a Solution

To check Simple harmonic motion first ,I have to displace the mass by some distance which I take to be x in this case.

Therefore the spring will be displaced by a distance 2x and a spring force of 2kx will act on the pulley from the spring since it is massless and hence due to Third law of motion I think.I don't know how to proceed after this

 

[Orodruin]

Therefore the spring will be displaced by a distance 2x

You need to rethink this.

 

[Hydrous Caperilla]

You need to rethink this.

I got struck after this...I need to know how the Third law will affect the pulley more after this but I can't get a clear idea of that

 

[Orodruin]

I got struck after this

You misunderstand me. Your statement was wrong, so you need to rethink it.

Apart from that, what do you get when you apply the third law to different subsystems, for example, the pulley, the mass, etc?

 

[Hydrous Caperilla]

I have no idea about that...

 

[Orodruin]

I am sorry, but we can only show you the path. You need to walk it yourself.

What exactly is your difficulty in writing down the forces that act on, for example, the pulley?

 

[Hydrous Caperilla]

The pulley will feel spring force due to the elongation of spring but How would this force be countered...I f I get that then this will probably help me a lot

 

[Orodruin]

You are missing some of the forces that act on the pulley. Note that we are only talking about the pulley now. Not the system as a whole, only the pulley subsystem.

 

[Hydrous Caperilla]

You are missing some of the forces that act on the pulley. Note that we are only talking about the pulley now. Not the system as a whole, only the pulley subsystem.

So will it balanced by Tension

 

[Orodruin]

Yes, so how does Newton's third law look for the pulley?

 

[Hydrous Caperilla]

Both sides of pulley will experience a force of kx/4 to counter the force(I messed up the spring force on pulley)

 

[Hydrous Caperilla]

Both sides of pulley will experience a force of kx/4 to counter the force(I messed up the spring force on pulley)

 

[Orodruin]

So what does this mean for the force balance of the mass?

 

[Hydrous Caperilla]

So now the mass will feel mg-kx/4 force at the displaced position

 

[Orodruin]

Which means what for the equation of motion?