engnrshyckh
- 51
- 2
the following 2nd order differential equation is given:
2y'' + 4y' +8y=8x........(1)
i want to find damping ratio, undamped natural frequency, damping ratio coefficient and time constant for the above system.
solution:
comparimg (1) with general system equaion
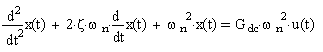
(veriable can be exchanged)
{where: x(t) = Response of the System,
u(t) = Input to the System,
z = Damping Ratio,
wn=Undamped Natural Frequency,
Gdc= The DC Gain of the System.}
damping ratio z or zeta:
2zw=2
w=2 so z=2/4=0.5
undamped natural frequency w or omega:
w=2 but correct ans is 1. any help?
2y'' + 4y' +8y=8x........(1)
i want to find damping ratio, undamped natural frequency, damping ratio coefficient and time constant for the above system.
solution:
comparimg (1) with general system equaion
(veriable can be exchanged)
{where: x(t) = Response of the System,
u(t) = Input to the System,
z = Damping Ratio,
wn=Undamped Natural Frequency,
Gdc= The DC Gain of the System.}
damping ratio z or zeta:
2zw=2
w=2 so z=2/4=0.5
undamped natural frequency w or omega:
w=2 but correct ans is 1. any help?